
【题目】如图,是某种蜡烛在燃烧过程中高度与时间之间关系的图像,由图像解答下列问题:
(1)此蜡烛燃烧1小时后,高度为 cm;经过 小时燃烧完毕;
(2)求这个蜡烛在燃烧过程中高度与时间之间关系的解析式.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
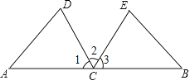
(1)求证:△ACD≌△BCE;
(2)若∠D=75°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
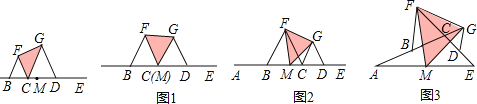
【题目】在图1至图3中,点B是线段AC的中点,点D是CE的中点,△BCF和△CDG都是等边三角形,点M为AE的中点,连接FG.
(1)如图1,若点E在AC的延长线上,点M与点C重合,则△FMG 等边三角形(填“是”或“不是”)
(2)将图1中的CE缩短,得到图2.求证:△FMG为等边三角形;
(3)将图2中的CE绕点E顺时针旋转一个锐角,得到图3.求证:△FMG为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
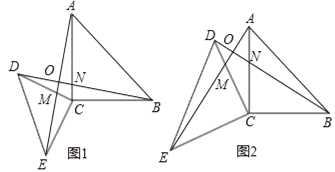
【题目】已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N.
(1)如图1,猜想AE与BD的数量关系与位置关系,并加以证明.
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
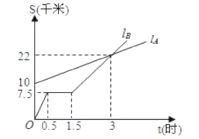
(1)B出发时与A相距___千米。
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是___小时。
(3)B出发后___小时与A相遇。
(4)若B的自行车不发生故障,保持出发时的速度前进,___小时与A相遇,相遇点离B的出发点___千米。在图中表示出这个相遇点C.
查看答案和解析>>
科目:初中数学 来源: 题型:
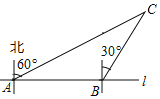
【题目】如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.
(1)求景点B与C的距离;
(2)为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们一般先仔细读题干,找出有用信息作为已知条件,然后用这些信息解决问题,但是有的题目信息比较明显,我们把这样的信息称为显性条件,而有的信息不太明显需要结合图形,特殊式子成立的条件,实际问题等发现隐含信息作为条件,这样的条件称为隐含条件,所以我们在做题时更注意发现题目中的隐含条件
(阅读理解)
读下面的解题过程,体会加何发现隐含条件,并回答.
化简:![]() .解:隐含条件1-3x≥0,解得:x
.解:隐含条件1-3x≥0,解得:x![]() ,∴原式=(1-3x)-(1-x)=1-3x-1+x=-2x
,∴原式=(1-3x)-(1-x)=1-3x-1+x=-2x
(启发应用)
已知△ABC三条边的长度分别是![]() ,记△ABC的周长为C△ABC
,记△ABC的周长为C△ABC
(1)当x=2时,△ABC的最长边的长度是______(请直接写出答案).
(2)请求出C△ABC(用含x的代数式表示,结果要求化简).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(情境)某课外兴趣小组在一次折纸活动课中.折叠一张带有条格的长方形的纸片ABCD(如图1),将点B分别与点A,A1,A2,…,D重合,然后用笔分别描出每条折痕与对应条格线所在的直线的交点,用平滑的曲线顺次连结各交点,得到一条曲线.
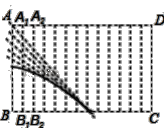
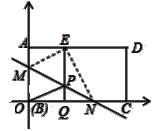
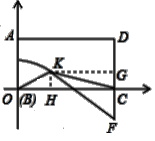
图1 图2 图3
(探索)(1)如图2,在平面直角坐标系xOy中,将矩形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB边放在y轴的正半轴上,AB=m,AD=n,(m≤n).将纸片折叠,使点B落在边AD上的点E处,过点E作EQ⊥BC于点Q,折痕MN所在直线与直线EQ相交于点P,连结OP.求证:四边形OMEP是菱形;
(归纳)(2)设点P坐标是(x,y),求y与x的函数关系式(用含m的代数式表示).
(运用)(3)将矩形纸片ABCD如图3放置,AB=8,AD=12,将纸片折叠,当点B与点D重合时,折痕与DC的延长线交于点F.试问在这条折叠曲线上是否存在点K,使得△KCF的面积是△KOC面积的![]() ?若存在,写出点K的坐标;若不存在,请说明理由.
?若存在,写出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )
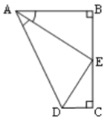
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com