
【题目】(情境)某课外兴趣小组在一次折纸活动课中.折叠一张带有条格的长方形的纸片ABCD(如图1),将点B分别与点A,A1,A2,…,D重合,然后用笔分别描出每条折痕与对应条格线所在的直线的交点,用平滑的曲线顺次连结各交点,得到一条曲线.
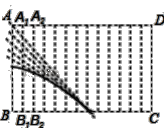
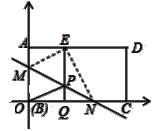
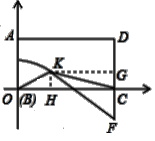
图1 图2 图3
(探索)(1)如图2,在平面直角坐标系xOy中,将矩形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB边放在y轴的正半轴上,AB=m,AD=n,(m≤n).将纸片折叠,使点B落在边AD上的点E处,过点E作EQ⊥BC于点Q,折痕MN所在直线与直线EQ相交于点P,连结OP.求证:四边形OMEP是菱形;
(归纳)(2)设点P坐标是(x,y),求y与x的函数关系式(用含m的代数式表示).
(运用)(3)将矩形纸片ABCD如图3放置,AB=8,AD=12,将纸片折叠,当点B与点D重合时,折痕与DC的延长线交于点F.试问在这条折叠曲线上是否存在点K,使得△KCF的面积是△KOC面积的![]() ?若存在,写出点K的坐标;若不存在,请说明理由.
?若存在,写出点K的坐标;若不存在,请说明理由.
【答案】(1)见解析 (2)y=![]() (3)点K(2+2
(3)点K(2+2![]() ,
,![]() )
)
【解析】(1)、如果四边形的四边相等,那么这个四边形是菱形;(2)、根据P点的坐标,可表示出E点的坐标,从而可知道OP的长,用勾股定理表示出解析式;(3)、首先画出图形,作KG⊥DC于G,KH⊥OC于H.设K(x,y),根据面积的关系得出y=![]() ,将点K的坐标代入二次函数解析式,从而得出x的值,得出点K的坐标.
,将点K的坐标代入二次函数解析式,从而得出x的值,得出点K的坐标.
(1)、证明:如图3,由题意知:OM=ME,∠OMN=∠EMN, ∵OM∥EP,∴∠OMN=∠MPE.
∴∠EMN=∠MPE. ∴ME=EP.∴OM=EP. ∴四边形OMEP是平行四边形.
又∵ME=EP,∴四边形OMEP是菱形;
(2)、解:∵四边形OMEP是菱形, ∴OP=PE,∴OP2=PE2, ∵EQ=OA=m,PQ=y,
∴PE=m﹣y.∴PE2=(m﹣y)2=m2﹣2my+y2.
∵OP2=x2+y2,PE2=m2﹣2my+y2, ∴x2+y2=m2﹣2my+y2. ∴y=![]() ;
;
(3)、解:如图3,假设折叠曲线上存在点K满足条件.
当m=8时,y=﹣![]() x2+4. 作KG⊥DC于G,KH⊥OC于H.设K(x,y),
x2+4. 作KG⊥DC于G,KH⊥OC于H.设K(x,y),
则KG=12﹣x,KH=y. 当x=12时,y=﹣5. ∴F(12,﹣5), ∴CF=5.
∴S△KCF=![]() CF×KG=
CF×KG=![]() ×5×(12﹣x), S△KOC=
×5×(12﹣x), S△KOC=![]() CO×KH=
CO×KH=![]() ×12y, ∵S△KCF=
×12y, ∵S△KCF=![]() S△KOC,
S△KOC,
∴0.5×5·(12-x)=![]() ×
×![]() ×12·y ∴y=
×12·y ∴y=![]() . ∴K(x,
. ∴K(x,![]() ).
).
∵点K在y=﹣![]() x2+4上, ∴
x2+4上, ∴![]() =﹣
=﹣![]() x2+4. 化简得:x2﹣4x﹣16=0,
x2+4. 化简得:x2﹣4x﹣16=0,
解得:x1=2+2![]() ,x2=2﹣2
,x2=2﹣2![]() (舍去), 当x1=2+2
(舍去), 当x1=2+2![]() 时,y=
时,y=![]() ,
,
∴存在点K(2+2![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
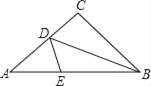
【题目】如图,三角形纸牌中,AB=8cm,BC=6cm,AC=5cm,沿着过△ABC的顶点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED周长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某种蜡烛在燃烧过程中高度与时间之间关系的图像,由图像解答下列问题:
(1)此蜡烛燃烧1小时后,高度为 cm;经过 小时燃烧完毕;
(2)求这个蜡烛在燃烧过程中高度与时间之间关系的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() 、点
、点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)点![]() 表示的数是______.
表示的数是______.
(2)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 到达点
到达点![]() 处?
处?
(3)点![]() 表示的数是______(用含字母
表示的数是______(用含字母![]() 的式子表示)
的式子表示)
(4)求当![]() 等于多少秒时,
等于多少秒时,![]() 、
、![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水泥厂的仓库![]() 天内进出库的吨数记录如下(+表示进库,-表示出库):
天内进出库的吨数记录如下(+表示进库,-表示出库):![]()
(1)经过这![]() 天,水泥仓库里的水泥是增多了还是减少了?增多或减少了多少吨?
天,水泥仓库里的水泥是增多了还是减少了?增多或减少了多少吨?
(2)经过这![]() 天,水泥仓库管理员结算时发现还库存有
天,水泥仓库管理员结算时发现还库存有![]() 吨水泥,那么
吨水泥,那么![]() 天前水泥仓库里存有水泥多少吨?
天前水泥仓库里存有水泥多少吨?
(3)如果进仓库的水泥每吨运费为![]() 元,出仓库的水泥每吨运费为
元,出仓库的水泥每吨运费为![]() 元,那么这
元,那么这![]() 天共要付多少元运费?
天共要付多少元运费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=x+1交x轴于点A,交y轴于点A1,A2,A3,…在直线l上,点B1,B2,B3…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn,顶点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰![]() 中,
中,![]() ,点A、B分别在坐标轴上.
,点A、B分别在坐标轴上.
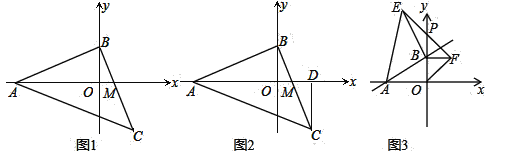
(1)如图1,若![]() ,
,![]() ,求C点的坐标;
,求C点的坐标;
(2)如图2,CD垂直x轴于D点,判断CD、OA、OD的数量关系,并证明你的结论;
(3)如图3,若点A的坐标为![]() ,点B在y轴的正半轴上运动时,分别以OB,AB为边在第一,第二象限作等腰
,点B在y轴的正半轴上运动时,分别以OB,AB为边在第一,第二象限作等腰![]() ,等腰
,等腰![]() ,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度是否变化?如果不变求出PB值,如果变化求PB的取值范围.
,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度是否变化?如果不变求出PB值,如果变化求PB的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3.
y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+![]() A)﹣(2b+
A)﹣(2b+![]() B)的值.
B)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com