
【题目】某水泥厂的仓库![]() 天内进出库的吨数记录如下(+表示进库,-表示出库):
天内进出库的吨数记录如下(+表示进库,-表示出库):![]()
(1)经过这![]() 天,水泥仓库里的水泥是增多了还是减少了?增多或减少了多少吨?
天,水泥仓库里的水泥是增多了还是减少了?增多或减少了多少吨?
(2)经过这![]() 天,水泥仓库管理员结算时发现还库存有
天,水泥仓库管理员结算时发现还库存有![]() 吨水泥,那么
吨水泥,那么![]() 天前水泥仓库里存有水泥多少吨?
天前水泥仓库里存有水泥多少吨?
(3)如果进仓库的水泥每吨运费为![]() 元,出仓库的水泥每吨运费为
元,出仓库的水泥每吨运费为![]() 元,那么这
元,那么这![]() 天共要付多少元运费?
天共要付多少元运费?
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
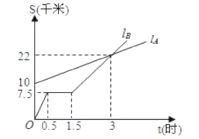
(1)B出发时与A相距___千米。
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是___小时。
(3)B出发后___小时与A相遇。
(4)若B的自行车不发生故障,保持出发时的速度前进,___小时与A相遇,相遇点离B的出发点___千米。在图中表示出这个相遇点C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们一般先仔细读题干,找出有用信息作为已知条件,然后用这些信息解决问题,但是有的题目信息比较明显,我们把这样的信息称为显性条件,而有的信息不太明显需要结合图形,特殊式子成立的条件,实际问题等发现隐含信息作为条件,这样的条件称为隐含条件,所以我们在做题时更注意发现题目中的隐含条件
(阅读理解)
读下面的解题过程,体会加何发现隐含条件,并回答.
化简:![]() .解:隐含条件1-3x≥0,解得:x
.解:隐含条件1-3x≥0,解得:x![]() ,∴原式=(1-3x)-(1-x)=1-3x-1+x=-2x
,∴原式=(1-3x)-(1-x)=1-3x-1+x=-2x
(启发应用)
已知△ABC三条边的长度分别是![]() ,记△ABC的周长为C△ABC
,记△ABC的周长为C△ABC
(1)当x=2时,△ABC的最长边的长度是______(请直接写出答案).
(2)请求出C△ABC(用含x的代数式表示,结果要求化简).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在“元旦”期间对顾客实行优惠,规定一次性购物优惠办法:
少于200元,不予优惠;高于200元但低于500元时,九折优惠;消费500元或超过500元时,其中500元部分给予九折优惠,超过500元部分给予八折优惠.根据优惠条件完成下列任务:
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款0.9x,当x大于或等于500元时,他实际付款多少元?(用含x的代数式表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的式子表示王老师两次购物实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(情境)某课外兴趣小组在一次折纸活动课中.折叠一张带有条格的长方形的纸片ABCD(如图1),将点B分别与点A,A1,A2,…,D重合,然后用笔分别描出每条折痕与对应条格线所在的直线的交点,用平滑的曲线顺次连结各交点,得到一条曲线.
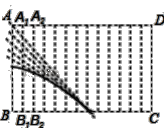
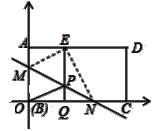
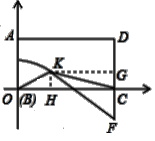
图1 图2 图3
(探索)(1)如图2,在平面直角坐标系xOy中,将矩形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB边放在y轴的正半轴上,AB=m,AD=n,(m≤n).将纸片折叠,使点B落在边AD上的点E处,过点E作EQ⊥BC于点Q,折痕MN所在直线与直线EQ相交于点P,连结OP.求证:四边形OMEP是菱形;
(归纳)(2)设点P坐标是(x,y),求y与x的函数关系式(用含m的代数式表示).
(运用)(3)将矩形纸片ABCD如图3放置,AB=8,AD=12,将纸片折叠,当点B与点D重合时,折痕与DC的延长线交于点F.试问在这条折叠曲线上是否存在点K,使得△KCF的面积是△KOC面积的![]() ?若存在,写出点K的坐标;若不存在,请说明理由.
?若存在,写出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
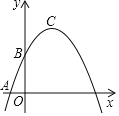
【题目】在平面直角坐标系xOy中(如图).已知抛物线y=﹣![]() x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0,![]() ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求这条抛物线的表达式;
(2)求线段CD的长;
(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com