
【题目】如图,点P是△ABC的外角∠EAB的平分线AF上的一点,PD垂直平分BC,PG![]() AB,求证:BG=AG+AC.
AB,求证:BG=AG+AC.
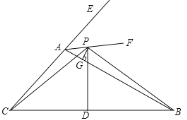
【答案】证明见解析.
【解析】
作HP⊥CE,H为垂足,根据角平分线的性质得到PH=PG,推出Rt△APH≌Rt△APG,根据全等三角形的性质得到AH=AG,由PD垂直平分BC,得到PC=PB,证得Rt△PHC≌Rt△PGB,于是得到CH=BG,等量代换即可得到结论.
证明:作HP⊥CE,H为垂足,
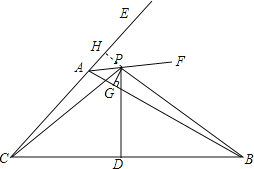
∵点P是△ABC的外角∠EAB的平分线AF上的一点,PG⊥AB,
∴PH=PG,
在Rt△APH与Rt△APG中,
![]() ,
,
∴Rt△APH≌Rt△APG,
∴AH=AG,
∵PD垂直平分BC,
∴PC=PB,
在Rt△PHC与Rt△PGB中,
![]() ,
,
∴Rt△PHC≌Rt△PGB,
∴CH=BG,
∵CH=AC+AH=AC+AG,
∴BG=AG+AC.


科目:初中数学 来源: 题型:
【题目】某厂一周计划每天生产200辆电动车,由于各种原因,实际每天的产量与计划相比有出入,下表是某周生产情况(超产为正,减产为负)
星期 | 一 | 二 | 三 | 四 | 五 |
增减 | +5 | -2 | -4 | +13 | -10 |
(1)产量最多一天是 辆,最少的一天是 辆.
(2)这一周一共生产了多少辆?
(3)该工厂按天计件计算工资,每生产一辆可得50元,若每超额一辆另奖15元,每少生产一辆另扣30元,那么该厂工人本周前三天的工资是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线经过点A(-3,0),点B(0,
中,直线经过点A(-3,0),点B(0,![]() ),点P的坐标为(1,0),与
),点P的坐标为(1,0),与![]() 轴相切于点O,若将⊙P沿
轴相切于点O,若将⊙P沿![]() 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
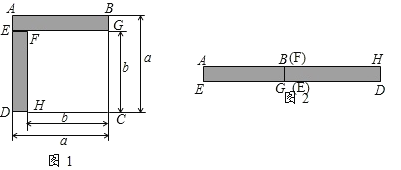
(1)如图1,已知正方形![]() 的边长为
的边长为![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,长方形
,长方形![]() 和
和![]() 为阴影部分,则阴影部分的面积是____.(写成平方差的形式)
为阴影部分,则阴影部分的面积是____.(写成平方差的形式)
(2)将图1中的长方形![]() 和
和![]() 剪下来,拼成图2所示的长方形,则长方形
剪下来,拼成图2所示的长方形,则长方形![]() 的面积是____.(写成多项式相乘的形式)
的面积是____.(写成多项式相乘的形式)
(3)比较图1与图2的阴影部分的面积,可得乘法公式____.
(4)利用所得公式计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
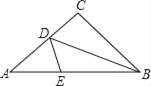
【题目】如图,三角形纸牌中,AB=8cm,BC=6cm,AC=5cm,沿着过△ABC的顶点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED周长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,C点在y轴上,B点在x轴上,A点从C点出发沿正西运动,B点在x轴上运动.

(1)如图1当∠ABC=∠ABD,作∠CBO的平分线交AC的延长线于E,作CF⊥EB于F.求证:∠ABD=∠ECF;
(2)如图2,在(1)的条件下,延长AB与∠BCO的平分线交于M点,下列结论:
①∠M的度数不变;
②∠ABC﹣∠M的值不变,可以证明只有一个结论正确,请你作出正确的选择并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
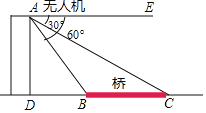
【题目】小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度AD,小亮通过操控器指令无人机测得桥头B,C的俯角分别为∠EAB=60°,∠EAC=30°,且D,B,C在同一水平线上.已知桥BC=30米,求无人机飞行的高度AD.(精确到0.01米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水泥厂的仓库![]() 天内进出库的吨数记录如下(+表示进库,-表示出库):
天内进出库的吨数记录如下(+表示进库,-表示出库):![]()
(1)经过这![]() 天,水泥仓库里的水泥是增多了还是减少了?增多或减少了多少吨?
天,水泥仓库里的水泥是增多了还是减少了?增多或减少了多少吨?
(2)经过这![]() 天,水泥仓库管理员结算时发现还库存有
天,水泥仓库管理员结算时发现还库存有![]() 吨水泥,那么
吨水泥,那么![]() 天前水泥仓库里存有水泥多少吨?
天前水泥仓库里存有水泥多少吨?
(3)如果进仓库的水泥每吨运费为![]() 元,出仓库的水泥每吨运费为
元,出仓库的水泥每吨运费为![]() 元,那么这
元,那么这![]() 天共要付多少元运费?
天共要付多少元运费?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com