
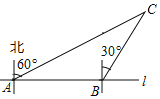
【题目】如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.
(1)求景点B与C的距离;
(2)为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
【答案】(1)10km;(2)![]() km.
km.
【解析】(1)先根据方向角的定义得出∠CAB=30°,∠ABC=120°,由三角形内角和定理求出∠C=180°﹣∠CAB﹣∠ABC=30°,则∠CAB=∠C=30°,根据等角对等边求出BC=AB=10km;
(2)首先过点C作CE⊥AB于点E,然后在Rt△CBE中,求得答案即可.
(1)如图,由题意得∠CAB=30°,∠ABC=90°+30°=120°,
∴∠C=180°﹣∠CAB﹣∠ABC=30°,
∴∠CAB=∠C=30°,
∴BC=AB=10km,
即景点B、C相距的路程为10km;
(2)如图,过点C作CE⊥AB于点E,
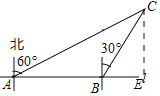
∵BC=10km,C位于B的北偏东30°的方向上,
∴∠CBE=60°,
在Rt△CBE中,CE=![]() BC=5
BC=5![]() km.
km.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点B、C、D、E在同一条直线上,已知AB = FC,AD = FE, BC=DE.
(1)求证:△ABD≌△FCE.
(2)AB与FC的位置关系是_________(请直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD>AB,点P是CD边上的任意一点(不含C,D两端点),过点P作PF∥BC,交对角线BD于点F.
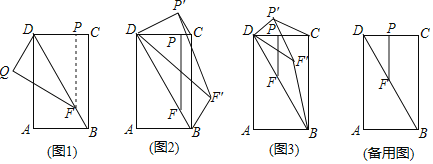
(1)如图1,将△PDF沿对角线BD翻折得到△QDF,QF交AD于点E.求证:△DEF是等腰三角形;
(2)如图2,将△PDF绕点D逆时针方向旋转得到△P'DF',连接P'C,F'B.设旋转角为α(0°<α<180°).
①若0°<α<∠BDC,即DF'在∠BDC的内部时,求证:△DP'C∽△DF'B.
②如图3,若点P是CD的中点,△DF'B能否为直角三角形?如果能,试求出此时tan∠DBF'的值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某种蜡烛在燃烧过程中高度与时间之间关系的图像,由图像解答下列问题:
(1)此蜡烛燃烧1小时后,高度为 cm;经过 小时燃烧完毕;
(2)求这个蜡烛在燃烧过程中高度与时间之间关系的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() 、点
、点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)点![]() 表示的数是______.
表示的数是______.
(2)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 到达点
到达点![]() 处?
处?
(3)点![]() 表示的数是______(用含字母
表示的数是______(用含字母![]() 的式子表示)
的式子表示)
(4)求当![]() 等于多少秒时,
等于多少秒时,![]() 、
、![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=x+1交x轴于点A,交y轴于点A1,A2,A3,…在直线l上,点B1,B2,B3…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn,顶点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,当点Q的运动速度为 时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com