
【题目】如图,点B、C、D、E在同一条直线上,已知AB = FC,AD = FE, BC=DE.
(1)求证:△ABD≌△FCE.
(2)AB与FC的位置关系是_________(请直接写出结论)

科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠BAC=90°,AB=AC,点P为AC上一点,M为BC上一点.
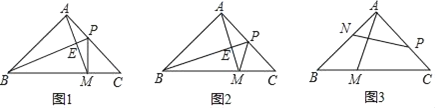
(1)若AM⊥BP于点E.
①如图1,BP为△ABC的角平分线,求证:PA=PM;
②如图2,BP为△ABC的中线,求证:BP=AM+MP.
(2)如图3,若点N在AB上,AN=CP,AM⊥PN,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
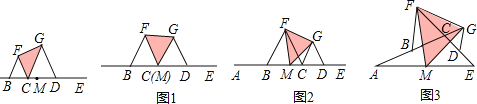
【题目】在图1至图3中,点B是线段AC的中点,点D是CE的中点,△BCF和△CDG都是等边三角形,点M为AE的中点,连接FG.
(1)如图1,若点E在AC的延长线上,点M与点C重合,则△FMG 等边三角形(填“是”或“不是”)
(2)将图1中的CE缩短,得到图2.求证:△FMG为等边三角形;
(3)将图2中的CE绕点E顺时针旋转一个锐角,得到图3.求证:△FMG为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

查看答案和解析>>
科目:初中数学 来源: 题型:
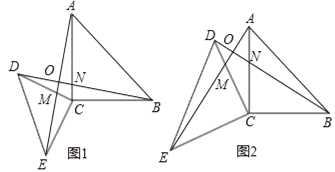
【题目】已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N.
(1)如图1,猜想AE与BD的数量关系与位置关系,并加以证明.
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
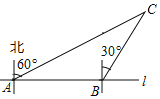
【题目】如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.
(1)求景点B与C的距离;
(2)为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
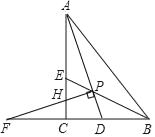
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com