
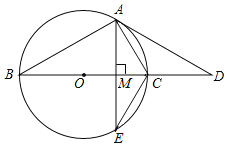
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】(1)先求出∠ABC=30°,进而求出∠BAD=120°,即可求出∠OAB=30°,结论得证;
(2)先求出∠AOC=60°,用三角函数求出AM,再用垂径定理即可得出结论.
(1)如图,
∵∠AEC=30°,
∴∠ABC=30°,
∵AB=AD,
∴∠D=∠ABC=30°,
根据三角形的内角和定理得,∠BAD=120°,
连接OA,∴OA=OB,
∴∠OAB=∠ABC=30°,
∴∠OAD=∠BAD﹣∠OAB=90°,
∴OA⊥AD,
∵点A在⊙O上,
∴直线AD是⊙O的切线;
(2)连接OA,∵∠AEC=30°,
∴∠AOC=60°,
∵BC⊥AE于M,
∴AE=2AM,∠OMA=90°,
在Rt△AOM中,AM=OAsin∠AOM=4×sin60°=2![]() ,
,
∴AE=2AM=4![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
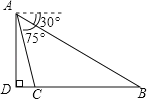
【题目】如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
A. 300(![]() +1)m B. 1200(
+1)m B. 1200(![]() ﹣1)m C. 1800(
﹣1)m C. 1800(![]() ﹣1)m D. 2400(
﹣1)m D. 2400(![]() ﹣1)m
﹣1)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,抛物线的顶点为P.
(1)如图1,连接AP,分别求出抛物线与直线AP的解析式;
(2)如图1,点D(2,3)在抛物线上,在第一象限内,直线AP上是否存在点E,使DE⊥EO?若存在,求出点E的坐标;若不存在,请说明理由.
(3)如图2,连接BC与抛物线的对称轴交于点F,在对称轴右侧的抛物线上是否存在点G,使△GPF与△GBF的面积相等?若存在,求出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
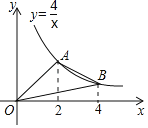
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数y=![]() 的图象与性质.
的图象与性质.
因为y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我们对比函数y=﹣
+1,所以我们对比函数y=﹣![]() 来探究.
来探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y=![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y=![]() 的图象是由y=﹣
的图象是由y=﹣![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设A(x1,y1),B(x2,y2)是函数y=![]() 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
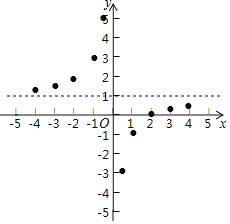
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个数值转换器的原理如图所示:若开始输入x的值是1,第1次输出的结果是4,第2次输出的结果是2,依次继续下去,则第2020次输出的结果是( )
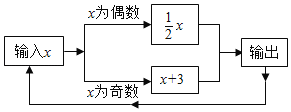
A.1010B.4C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
(应用):
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
(拓展):
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)已知E(2,0),若F(﹣1,﹣2),求d(E,F);
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,求t的值;
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,求d(P,Q).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数
![]() ①
①
![]() ②
②
![]() ③
③
![]() 第①行的第
第①行的第![]() 个数可表示为 ;
个数可表示为 ;
![]() 第②③行数与第①行数分别有什么关系?
第②③行数与第①行数分别有什么关系?
![]() 取每行的第
取每行的第![]() 个数,从上到下依次把这三个数记为
个数,从上到下依次把这三个数记为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com