【题目】如图，AD∥BC，∠BAC＝70°，DE⊥AC于点E，∠D＝20°.
(1)求∠B的度数，并判断△ABC的形状；
(2)若延长线段DE恰好过点B，试说明DB是∠ABC的平分线．
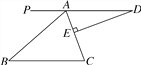
【答案】（1）△ABC是等腰三角形，∠B＝40°；（2）见解析.
【解析】(1)、根据Rt△ADE的内角和得出∠DAC=70°，根据平行线的性质得出∠C=70°，从而根据有两个角相等的三角形是等腰三角形得出答案；(2)、根据等腰三角形底边上的三线合一定理得出DB为顶角的角平分线．
解：(1)∵DE⊥AC于点E，∠D＝20°，∴∠CAD＝70°， ∵AD∥BC，
∴∠C＝∠CAD＝70°， 又∵∠BAC＝70°，∴∠BAC＝∠C，∴AB＝BC，
∴△ABC是等腰三角形，∴∠B＝180°－∠BAC－∠C＝180°－70°－70°＝40°.
(2)∵延长线段DE恰好过点B，DE⊥AC，∴BD⊥AC，∵△ABC是等腰三角形，
∴DB是∠ABC的平分线．
科目：初中数学 来源： 题型：
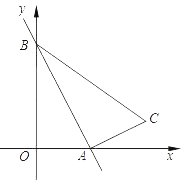
【题目】已知一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B，以AB为边在第一象限内作直角三角形ABC，且∠BAC=90°，tan∠ABC=
．
（1）求点C的坐标；
（2）在第一象限内有一点M（1，m），且点M与点C位于直线AB的同侧，使得2S△ABM=S△ABC，求点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小马虎做一道数学题，“已知两个多项式
，
，试求
.”其中多项式
的二次项系数印刷不清楚.
（1）小马虎看答案以后知道
，请你替小马虎求出系数“
”；
（2）在（1）的基础上，小马虎已经将多项式正确求出，老师又给出了一个多项式
，要求小马虎求出
的结果.小马虎在求解时，误把“”看成“
”，结果求出的答案为
.请你替小马虎求出“”的正确答案.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图 1，在正方形 ABCD 中，E，F 分别是 AD，CD 上两点，BE 交 AF 于点 G，且 DE＝CF．
（1）写出 BE 与 AF 之间的关系，并证明你的结论；
（2）如图 2，若 AB＝2，点 E 为 AD 的中点，求 AG 的长度。
（3）在（2）的条件下，连接 GD，试证明 GD 是∠EGF 的角平分线，并求出 GD 的长；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】魔术师为大家表演魔术. 他请观众想一个数，然后将这个数按以下步骤操作：
魔术师立刻说出观众想的那个数.
（1）如果小明想的数是-2，那么他告诉魔术师的结果应该是_________________；
（2）如果小聪想了一个数并告诉魔术师结果为9，那么魔术师立刻说出小聪想的那个数是 ；请解释魔术师是如何求出那个数的？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，过一点分别作坐标轴的垂线，若垂线与坐标轴围成矩形的周长与面积相等，则这个点叫做“和谐点”.
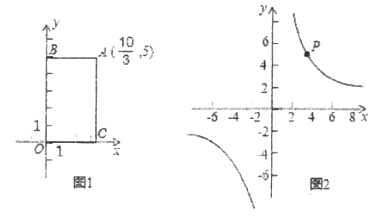
如图1，矩形ABOC的周长与面积相等，则点A是“和谐点”，
（1）点
，其中“和谐点”是_______；
（2）如图2，若点
是双曲线
上的“和谐点”，请直接写出所有满足条件的P点坐标__________________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知A(－4， 
)，B（-1,2）是一次函数y=kx+b与反比例函数y=
(m≠0，m＜0)图象的两个交点，AC⊥x轴于C，BD⊥y轴于D。
(1)、根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值?
(2)、求一次函数解析式及m的值；
(3)、P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，以△ABC的边AB为直径作⊙O，点C在⊙O上，BD是⊙O的弦，∠A=∠CBD，过点C作CF⊥AB于点F，交BD于点G，过C作CE∥BD交AB的延长线于点E．
（1）求证：CE是⊙O的切线；
（2）求证：CG=BG；
（3）若∠DBA=30°，CG=4，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从2开始，连续的偶数相加，它们和的情况如下表：
(1)若n=7时，则S的值为___.
(2)根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=___.
根据上题的规律计算：300+302+304+…+2016+2018+2020的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com