
【题目】在平面直角坐标系中,函数![]() 的图像记为
的图像记为![]() ,函数
,函数![]() 的图像记为
的图像记为![]() ,其中
,其中![]() 为常数,且
为常数,且![]() ,图像
,图像![]() 、
、![]() ,合起来得到的图像标记为
,合起来得到的图像标记为![]() .
.
(1)求图像![]() 与
与![]() 轴的交点坐标.
轴的交点坐标.
(2)当图像![]() 的最低点到
的最低点到![]() 轴距离为3时,求
轴距离为3时,求![]() 的值.
的值.
(3)当![]() 时,若点
时,若点![]() 在图像
在图像![]() 上,求
上,求![]() 的值.
的值.
(4)点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,连接
,连接![]() 与图像
与图像![]() 有两个交点时
有两个交点时![]() 的取值范围.
的取值范围.
【答案】(1)(![]() );(2)
);(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4)
;(4)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)令M1的函数值等于0,即求出x的两个解,取正数解.
(2)因为提到“最低点”,所以函数图象M1对应的抛物线开口向上,a>0,令顶点纵坐标=3即求出a的值.
(3)把点在图象M1或图象M2进行分类讨论,把a=1和y=-![]() 代入解析式即求出m的值.
代入解析式即求出m的值.
(4)把a>0和a<0时图象M的大致草图画出,根据图象观察和计算说明线段PQ所在位置对交点个数的影响,得到a的范围.
(1)当ax2-2ax-4a=0时,
∵a≠0,
∴x2-2x-4=0
解得:x1=1+![]() ,x2=1-
,x2=1-![]()
∵x≥0,
∴图象M1与x轴的交点坐标为(1+![]() ,0)
,0)
(2)∵y=ax2-2ax-4a=a(x-1)2-5a,且图象M1的最低点到x轴距离为3
∴a>0,
∴|-5a|=3,即-5a=-3
∴a=![]()
(3)当a=1时,点(m,![]() )在图象M上,
)在图象M上,
①若点在图象M1上,即m≥0,m22m4=![]()
解得:m1=1+![]() ,m2=1-
,m2=1-![]() (舍去)
(舍去)
②若点在图象M2上,即m<0,m22m+4=![]()
解得:m3=-1+![]() (舍去),m4=-1-
(舍去),m4=-1-![]()
综上所述,m的值为1+![]() 或-1-
或-1-![]()
(4)若a>0,则图象M的大致形状如图1,
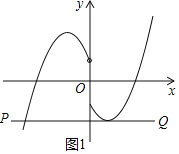
①若线段PQ经过图象M1的顶点(1,-5a)
则-5a=-1,得a=![]()
对于图象M2,-![]() x2-
x2-![]() x+
x+![]() =-1时,解得:x1=-1+
=-1时,解得:x1=-1+![]() (舍去),x2=-1-
(舍去),x2=-1-![]()
∵-1-![]() >-5
>-5
∴直线PQ与图象M2的交点在点P的右侧
∴线段PQ与图象M2有一个交点
∴a=![]() 时,线段PQ与图象M有两个交点
时,线段PQ与图象M有两个交点
②若线段PQ比图象M1与y轴交点高时,如图2,

则-4a<-1,解得:a>![]()
若a<0,则图象M的大致形状如图3,

③若线段PQ经过M2与y轴交点时,4a=-1 得a=![]() ,
,
对于图象M1,-![]() x2+
x2+![]() x+1=-1时,解得:x1=-2(舍去),x2=4,
x+1=-1时,解得:x1=-2(舍去),x2=4,
即此时线段PQ与图象M1交点为Q(4,-1),
∴当线段PQ比图象M2与y轴交点低时,与图象M2有两个交点,与图象M1没有交点,
最低不得低过图象M2的顶点(-1,5a),
∴5a<-1,
解得:a<![]() ,
,
综上所述,线段PQ与图象M有两个交点时,a=![]() 或a>
或a>![]() 或a<
或a<![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
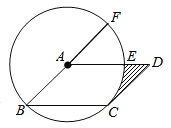
【题目】如图,在ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若弧EF的长为π,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
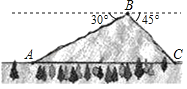
【题目】我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
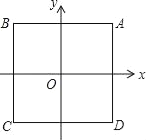
【题目】如图,在平面直角坐标系中,点O是边长为2的正方形ABCD的中心.函数y=(x﹣h)2的图象与正方形ABCD有公共点,则h的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的负半轴相交于点
轴的负半轴相交于点![]() ,将抛物线
,将抛物线![]() 平移得到抛物线
平移得到抛物线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,且
,且![]() .
.
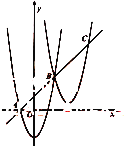
(1)求点![]() 的坐标;
的坐标;
(2)写出一种将抛物线![]() 平移到抛物线
平移到抛物线![]() 的方法;
的方法;
(3)在![]() 轴上找点
轴上找点![]() ,使得
,使得![]() 的值最小,求点
的值最小,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣
,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣![]() 或﹣
或﹣![]() .其中正确的有_____.(请将正确结论的序号全部填在横线上)
.其中正确的有_____.(请将正确结论的序号全部填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x![]() k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
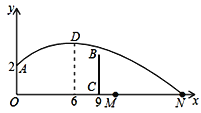
A. 球不会过网 B. 球会过球网但不会出界
C. 球会过球网并会出界 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇中学教学楼对面是一座小山,去年“联通”公司在山顶上建了座通讯铁塔.甲、乙两位同学想测出铁塔的高度,他们用测角器作了如下操作:甲在教学楼顶A处测得塔尖M的仰角为α,塔座N的仰角为β;乙在一楼B处只能望到塔尖M,测得仰角为θ(望不到底座),他们知道楼高AB=20m,通过查表得:tanα=0.5723,tanβ=0.2191,tanθ=0.7489;请你根据这几个数据,结合图形推算出铁塔高度MN的值.
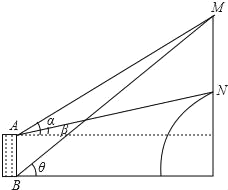
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com