
【题目】下列事件中,必然事件是( )
A.抛掷1个均匀的骰子,出现6点向上
B.两直线被第三条直线所截,同位角相等
C.366人中至少有2人的生日相同
D.实数的绝对值是非负数
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏的中奖概率是![]() , 则做5次这样的游戏一定会中奖
, 则做5次这样的游戏一定会中奖
B.为了解深圳中学生的心理健康情况,应该采用普查的方式
C.事件“小明今年中考数学考95分”是可能事件
D.若甲组数据的方差S![]() =0.01,乙组数据的方差S
=0.01,乙组数据的方差S![]() =0.1,则乙组数据更稳定
=0.1,则乙组数据更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
(1)可能性最大和最小的事件分别是哪个?(填写序号)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列: . 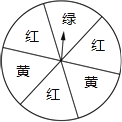
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=![]()
(1)李明第几天生产的粽子数量为420只?
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图形来刻画.若李明第x天创造的利润为w元,求w关于x的函数表达式,并求出第几天的利润最大,最大利润时多少元?(利润=出厂价﹣成本)
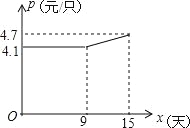
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投掷一枚均匀的硬币,落地时正面或反面向上的可能性相同.有甲、乙、丙三人做“投硬币”实验,他们分别投100次,结果正面向上的次数为:甲60次、乙40次、丙50次.则下列说法正确的是( )
A.甲第101次投出正面向上的概率最大
B.乙第101次投出正面向上的概率最大
C.只有丙第101次投出正面向上的概率为0.5
D.甲、乙、丙三人第101次投出正面向上的概率相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
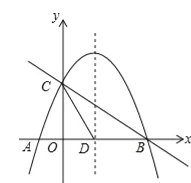
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com