
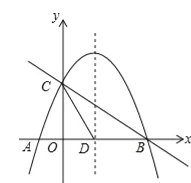
����Ŀ����ͼ��������y=��![]() x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
��3����Eʱ�߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ����CBF�������������CBF������������ʱE������꣮
���𰸡���1��y=��![]() x2+
x2+![]() x+2��2�����ڣ�
x+2��2�����ڣ�![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() ����3��4��E��2��1��
����3��4��E��2��1��
��������
�����������1����A����1��0����C��0��2������y=��![]() x2+bx+c�з����鼴�ɣ�
x2+bx+c�з����鼴�ɣ�
��2�������CD�ij������������ٵ�CP=CDʱ���ڵ�DC=DPʱ�ֱ���⼴�ɣ�
��3�����ֱ��BC�Ľ���ʽ����E![]() ����F
����F![]() ���������κ��������ö��κ��������ʼ��ɽ�����⣮
���������κ��������ö��κ��������ʼ��ɽ�����⣮
�����������1����A����1��0����C��0��2������y=��![]() x2+bx+c��
x2+bx+c��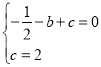 ��
��
���b=![]() ��c=2��
��c=2��
�������ߵĽ���ʽΪy=��![]() x2+
x2+![]() x+2��,
x+2��,
��2�����ڣ���ͼ1�У���C��0��2����D��![]() ��0����
��0����
��OC=2��OD=![]() ��CD=
��CD=![]() =
=![]()
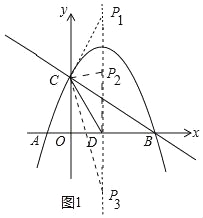
�ٵ�CP=CDʱ���ɵ�P1��![]() ��4����
��4����
�ڵ�DC=DPʱ���ɵ�P2��![]() ��
��![]() ����P3��
����P3��![]() ����
����![]() ��
��
��������������������P�������Ϊ![]() ����
����![]() ��
��![]() ������
������![]() ����
����![]() ����
����
��3����ͼ2�У�
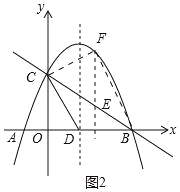
����������y=��![]() x2+
x2+![]() x+2����y=0ʱ����
x+2����y=0ʱ����![]() x2+
x2+![]() x+2=0�����x1=4��x2=��1
x+2=0�����x1=4��x2=��1
��B��4��0����A����1��0����
��B��4��0����C��0��2����ֱ��BC�Ľ���ʽΪy=��![]() x+2��
x+2��
��E![]() ��F
��F![]() ��
��
EF=![]() ��
��![]() =
=![]()
��-![]() ��0������m=2ʱ��EF�����ֵ2��
��0������m=2ʱ��EF�����ֵ2��
��ʱE��BC�е㣬
����E�˶���BC���е�ʱ����EBC������
���EBC������=![]() ��4��EF=
��4��EF=![]() ��4��2=4����ʱE��2��1����
��4��2=4����ʱE��2��1����


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��У���Ȼ�¼��ǣ�������
A.����1�����ȵ����ӣ�����6������
B.��ֱ�߱�������ֱ�����أ�ͬλ�����
C.366����������2�˵�������ͬ
D.ʵ���ľ���ֵ�ǷǸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
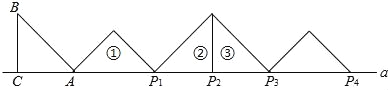
����Ŀ����ͼ������Rt��ABC�У���ACB=90�㣬AC=BC=1����AC����ֱ��a�ϣ�����ABC�Ƶ�A˳ʱ����ת��λ�âٿɵõ���P1����ʱAP1=![]() ����λ�âٵ��������Ƶ�P1˳ʱ����ת��λ�âڿɵõ���P2����ʱAP2=
����λ�âٵ��������Ƶ�P1˳ʱ����ת��λ�âڿɵõ���P2����ʱAP2=![]() +1����λ�âڵ��������Ƶ�P2˳ʱ����ת��λ�âۿɵõ���P3ʱ��AP3=
+1����λ�âڵ��������Ƶ�P2˳ʱ����ת��λ�âۿɵõ���P3ʱ��AP3=![]() +2�����˹��ɼ�����ת��ֱ���õ���P2026Ϊֹ����AP2016= ��
+2�����˹��ɼ�����ת��ֱ���õ���P2026Ϊֹ����AP2016= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��1����2���࣬��2����3��������1=58��������3=�� ��
A. 58�� B. 148�� C. 158�� D. 32��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD��BC��EF��ֱƽ��AC����AC�ڵ�F����BC�ڵ�E����BD=DE��
������BAE=40�������C�Ķ�����
������ABC�ܳ�13cm��AC=6cm����DC����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
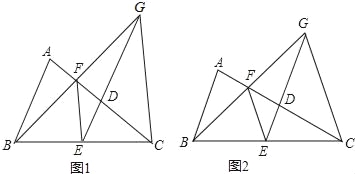
����Ŀ����ͼ����֪������ABC�У�AC=BC����D��E��F�ֱ����߶�AC��BC��AD���е㣬����FE��ED��BF���ӳ��߽�ED���ӳ����ڵ�G������GC��
��1����֤��EF��CG��
��2����AC=![]() AB����֤��AC=CG��
AB����֤��AC=CG��
��3����ͼ2����CG=EG����![]() = ��
= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
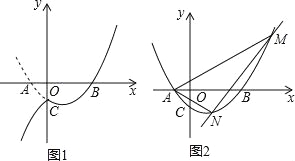
����Ŀ����֪������y=��m��1��x2+��m��2��x��1��x�ύ��A��B���㣬��m��1���ҵ�A�ڵ�B����࣬OA��OB=1��3
��1����ȷ�������ߵĽ���ʽ��
��2��ֱ��y=kx��3�������߽���M��N���㣬����AMN��������x���ϣ���k��ֵ��
��3���裨2������������y��Ľ���ΪC������C��ֱ��l��x�ᣬ����������y�����IJ�����ֱ��l���ۣ������ߵ����ಿ�ֱ��ֲ��䣬�õ�һ����ͼ����������ͼ��ش𣺵�ֱ��y=![]() x+b����ͼ��ֻ��һ��������P��x0��y0����y0��7ʱ����b��ȡֵ��Χ��
x+b����ͼ��ֻ��һ��������P��x0��y0����y0��7ʱ����b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��������չ��ͼ����֪�������������Ĵ���ʽ��ֵ��ȣ�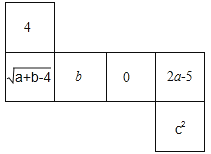
��1����a��b��c ��ֵ��
��2���ж�a+b��c��ƽ������������������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com