
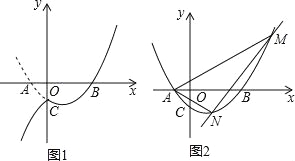
【题目】已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B两点,若m>1,且点A在点B的左侧,OA:OB=1:3
(1)试确定抛物线的解析式;
(2)直线y=kx﹣3与抛物线交于M、N两点,若△AMN的内心在x轴上,求k的值.
(3)设(2)中抛物线与y轴的交点为C,过点C作直线l∥x轴,将抛物线在y轴左侧的部分沿直线l翻折,抛物线的其余部分保持不变,得到一个新图象,请你结合新图象回答:当直线y=![]() x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1.
x﹣1.
(2)k=﹣3或![]() ;
;
(3)当﹣1<b≤7或b<﹣![]() 时直线y=
时直线y=![]() x+b与新图象只有一个公共点.
x+b与新图象只有一个公共点.
【解析】试题分析:(1)设A(﹣a,0),B(3a,0),根据根与系数关系可得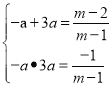 解方程组即可解决问题.
解方程组即可解决问题.
(2)设M(m,km﹣3),N(n,kn﹣3),显然m、n是方程:![]() x2﹣(k+
x2﹣(k+![]() )x+2=0的两根,得到m+n=3k+2,mn=6,再根据直线AM,直线AN两直线与x轴夹角相等,
)x+2=0的两根,得到m+n=3k+2,mn=6,再根据直线AM,直线AN两直线与x轴夹角相等,
即tan∠MAB=tan∠NAB,列出方程,整体代入即可求出k的值.
(3)直线y=![]() x+b与新图象只有一个公共点P(x0,y0)且y0≤7,所以b0≤7,又当直线y=
x+b与新图象只有一个公共点P(x0,y0)且y0≤7,所以b0≤7,又当直线y=![]() x+b经过点C(0,﹣1)时,b=﹣1,所以当﹣1<b≤7时,直线y=
x+b经过点C(0,﹣1)时,b=﹣1,所以当﹣1<b≤7时,直线y=![]() x+b与新图象只有一个公共点,由
x+b与新图象只有一个公共点,由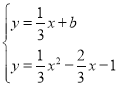 消去y得x2﹣3x﹣3﹣3b=0,当直线y=
消去y得x2﹣3x﹣3﹣3b=0,当直线y=![]() x+b与新图象只有一个公共点时,方程只有相等的实数根,根据△=0,列出方程求出b,由此即可解决问题.
x+b与新图象只有一个公共点时,方程只有相等的实数根,根据△=0,列出方程求出b,由此即可解决问题.
试题解析:(1)∵OA:OB=1:3,
∴可以假设A(﹣a,0),B(3a,0),
则有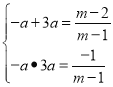 消去a得到3m2﹣16m+16=0,解得m=
消去a得到3m2﹣16m+16=0,解得m=![]() 或4(不合题意舍弃),
或4(不合题意舍弃),
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1.
x﹣1.
(2)设M(m,km﹣3),N(n,kn﹣3),
∵点M、N在抛物线上,则M(m,![]() m2﹣
m2﹣![]() m﹣1),N(n,
m﹣1),N(n,![]() n2﹣
n2﹣![]() n﹣1),
n﹣1),
∴km﹣3=![]() m2﹣
m2﹣![]() m﹣1,kn﹣3=
m﹣1,kn﹣3=![]() n2﹣
n2﹣![]() n﹣1,
n﹣1,
显然m、n是方程:![]() x2﹣(k+
x2﹣(k+![]() )x+2=0的两根,
)x+2=0的两根,
则m+n=3k+2,mn=6,
∵△CMN的内心在y轴上,A(﹣1,0),B(3,0),
∴直线AM,直线AN两直线与x轴夹角相等,
∴tan∠MAB=tan∠NAB
∴![]() ,
,
整理得到,2kmn+K(m+n)﹣3(m+n)﹣6=0,
∴12k+k(3k+2)﹣3(3k+2)=0,
解得k=﹣3或![]() .
.
(3)∵直线y=![]() x+b与新图象只有一个公共点P(x0,y0)且y0≤7,
x+b与新图象只有一个公共点P(x0,y0)且y0≤7,
∴b0≤7,
当直线y=![]() x+b经过点C(0,﹣1)时,b=﹣1,
x+b经过点C(0,﹣1)时,b=﹣1,
∴当﹣1<b≤7时,直线y=![]() x+b与新图象只有一个公共点,
x+b与新图象只有一个公共点,
由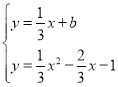 消去y得x2﹣3x﹣3﹣3b=0,
消去y得x2﹣3x﹣3﹣3b=0,
当直线y=![]() x+b与新图象只有一个公共点时,方程只有相等的实数根,△=0,
x+b与新图象只有一个公共点时,方程只有相等的实数根,△=0,
∴9+12+12b=0,
∴b=﹣![]() .
.
∴当b<﹣![]() 时,当直线y=
时,当直线y=![]() x+b与新图象只有一个公共点,
x+b与新图象只有一个公共点,
综上所述,当﹣1<b≤7或b<﹣![]() 时直线y=
时直线y=![]() x+b与新图象只有一个公共点.
x+b与新图象只有一个公共点.


科目:初中数学 来源: 题型:
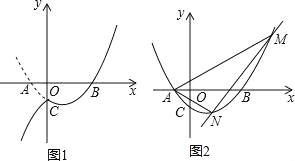
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
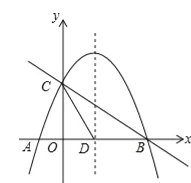
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月9日是第29个“消防宣传日”.某校举行“安全小能手”消防安全知识竞赛,有50位同学参加比赛,比赛结束后根据每个学生的最后得分计算出平均数、中位数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( ).
A.平均数B.中位数C.众数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“※”定义新运算:对于有理数a、b都有:a※b=ab-(a+b),那么5※3=__________;当m为有理数时,3※(m※2)=____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于x的方程中:①ax2+bx+c=0;②3(x﹣9)2﹣(x+1)2=1;③x+3=![]() ;④(a2+a+1)x2﹣a=0;(5)
;④(a2+a+1)x2﹣a=0;(5)![]() =x﹣1,一元二次方程的个数是( )
=x﹣1,一元二次方程的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com