解:(1)∵点A(m,m+1)、B(m+3,m-1)均在反比例函数y=

的图象上,
∴m(m+1)=(m+3)(m-1),
∴解得:m=3.
∴A(3,4)、B(6,2).
∴k=m(m+1)=12;
如图1,过A作AM⊥x轴于M,
则OM=3,AM=4,
∴AO=5.
根据反比例函数的对称性,AC=2AO=10;
(2)如图1,在y轴的正半轴上取OD=OA=5,连接AD、CD.
则OD=OA=OC.
则∠OCD=∠ODC,∠OAD=∠ODA.

在△ACD中,有∠ACD+∠ADC+∠CAD=180°.
即∠OCD+∠ODC+∠OAD+∠ODA=180°.
∴∠ODC+∠ODA=90°,
即∠ADC=90°.
∴D(0,5).
同理在y轴负半轴上还有点:D′(0,-5).
另法:如图1,设OD=t,由AD
2+CD
2=AC
2,
AE
2+ED
2+FD
2+CF
2=AC
2,
3
2+(t-4)
2+3
2+(t+4)
2=10
2,
解得:t=±5.
则D(0,5)或D′(0,-5).
(3)
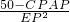
的值不发生变化,理由为:
如图2,连EO,过E作EN⊥x轴于N,过A作AM⊥x轴于M.
∵E(-4,3),A(3,4),
∴EO=OA=5,EN=OM=3,NO=AM=4,

在△ENO和△OMA中,
∵

,
∴△ENO≌△OMA(SSS),
∴∠EON=∠OAM,
∴∠EON+∠AOM=∠OAM+∠AOM=90°,
∴∠EOA=90°,
设CP=t,则AP=10-t,
CP•AP=t(10-t)=10t-t
2,
而EP
2=OP
2+EO
2=(5-t)
2+5
2=50-10t+t
2.
∴50-CP•AP=50-(10t-t
2)=50-10t+t
2.
∴50-CP•AP=EP
2,
∴
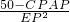
=1,
即
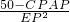
的值不发生变化,其值恒为1.
分析:(1)利用图象上点的性质将A,B分别代入解析式,即可得出m的值,再利用反比例函数的对称性得出AC的长即可;
(2)首先在y轴的正半轴上取OD=OA=5,连接AD、CD,利用等腰三角形的性质以及三角形内角和定理进而求出即可;
(3)利用已知首先证明△ENO≌△OMA,进而得出∠EOA=90°再利用勾股定理得出即可.
点评:此题主要考查了反比例函数的综合应用以及全等三角形的证明和勾股定理等知识,利用勾股定理表示出EP
2与CP•AP是解本题第二问的关键.

 的图象上,正比例函数y=nx的图象交反比例函数图象于A、C两点.
的图象上,正比例函数y=nx的图象交反比例函数图象于A、C两点.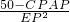 的值是否发生变化?若不变,求出其值;若变化,说明理由.
的值是否发生变化?若不变,求出其值;若变化,说明理由.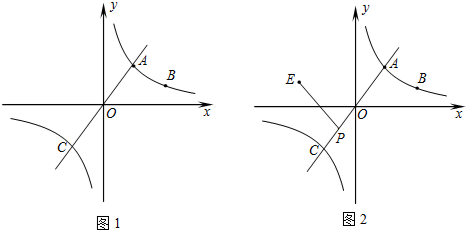
 的图象上,
的图象上,
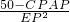 的值不发生变化,理由为:
的值不发生变化,理由为:
 ,
,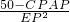 =1,
=1,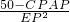 的值不发生变化,其值恒为1.
的值不发生变化,其值恒为1.

 (2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,cos∠AOB=
(2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,cos∠AOB=

