
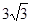 )是反比例函数y=
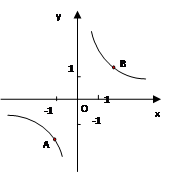
)是反比例函数y=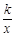 图像上的两个点,点C(-1,0),在此函数图像上找一点D,使得以A,B,C,D为顶点的四边形为梯形。满足条件的点D共有( )
图像上的两个点,点C(-1,0),在此函数图像上找一点D,使得以A,B,C,D为顶点的四边形为梯形。满足条件的点D共有( )| A.4个 | B.5个 | C.3个 | D.6个 |
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:不详 题型:解答题
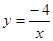
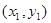 ,
,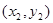 都在此反比例函数图象上且
都在此反比例函数图象上且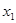 >
>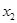 ,比较
,比较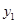 与
与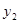 的大小(直接写出结果)
的大小(直接写出结果)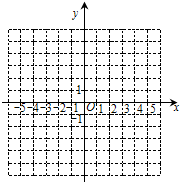
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
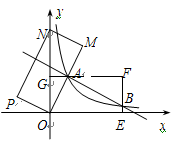
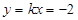 (
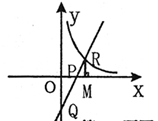
(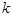 >0)与双曲线
>0)与双曲线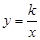 在第一象限内的交点面积为R,与
在第一象限内的交点面积为R,与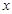 轴的交点为P,与
轴的交点为P,与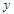 轴的交点为Q;作RM⊥
轴的交点为Q;作RM⊥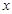 轴于点M,若△OPQ与△PRM的面积是4:1,则
轴于点M,若△OPQ与△PRM的面积是4:1,则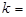
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
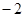 ,
,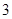 )、(
)、(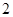 ,
,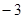 )、(
)、(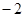 ,
,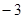 )、(
)、(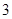 ,
,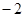 )、(
)、(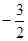 ,
,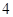 )五个点在同一个反比例函数的图像上,后来经检查发现其中有一个点不在,这个点是( )
)五个点在同一个反比例函数的图像上,后来经检查发现其中有一个点不在,这个点是( )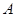 .(
.(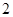 ,
,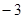 );
); 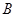 .(
.(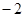 ,
,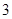 );
); 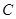 .(
.(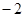 ,
,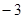 );
);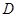 .(
.(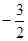 ,
,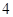 ).
).查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 在第一象限的图象,点A为此图象上的一动点,过点A分别作AB⊥x轴和AC⊥y轴,垂足分别为B,C.则四边形OBAC周长的最小值为【 】
在第一象限的图象,点A为此图象上的一动点,过点A分别作AB⊥x轴和AC⊥y轴,垂足分别为B,C.则四边形OBAC周长的最小值为【 】
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com