
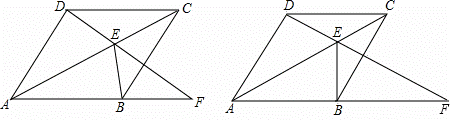
如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
(1)如果①:求证∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)
 [来源:学科网ZXXK]
[来源:学科网ZXXK]
(1)证明:∵四边形ABCD为菱形,
∴DC=CB,
在△DCE和△BCE中, 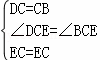 ,
,
∴△DCE≌△BCE(SAS), ∴∠EDC=∠EBC,
∵DC∥AB, ∴∠EDC=∠AFD, ∴∠AFD=∠EBC;
(2)解:∵DE=EC, ∴∠EDC=∠ECD,
设∠EDC=∠ECD=∠CBE=x°,则∠CBF=2x°, 由BE⊥AF得:2x+x=90°, 解得:x=30°,
∴∠DAB=∠CBF=60°;
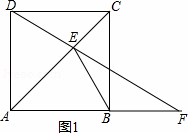
(3)分两种情况:
①如图1,当F在AB延长线上时,
∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
可通过三角形内角形为180°得:
90+x+x+x=180,
解得:x=30, ∴∠EFB=30°;
 ②如图2,当F在线段AB上时,
②如图2,当F在线段AB上时,
∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,
可证得:∠AFD=∠FDC=∠CBE,
得x+2x=90,
解得:x=30, ∴∠EFB=120°,
综上:∠EFB=30°或120°.
点评: 此题主要考查了四边形综合题,解题时,涉及到了菱形的性质、正方形的性质以及全等三角形的判定与性质等知识,利用分类讨论得出是解题关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
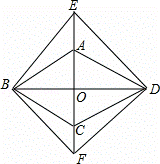
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
A. 了解飞行员视力的达标率应使用抽样调查
B. 一组数据3,6,6,7,9的中位数是6
C. 从2000名学生中选200名学生进行抽样调查,样本容量为2000
D. 掷一枚质地均匀的硬币,正面朝上是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
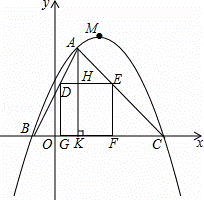
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
| x | … | ﹣2 | 0 | 4 | 8 | 10 | … |
| y | … | 0 | 5 | 9 | 5 | 0 | … |
(1)求出这条抛物线的解析式;
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为 米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com