
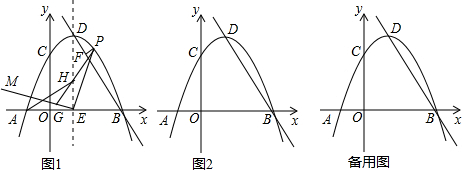
分析 (1)首先求出B、D两点坐标,再利用待定系数法即可解决问题;
(2)如图2中,设P(m,-$\frac{\sqrt{2}}{3}$m2+$\frac{4}{3}$m+2$\sqrt{2}$),连接PD、PB,作PQ⊥OB于Q.由题意欲求PF的最大值,易知当△PBD面积最大时,PF的值最大,由S△PBD=S△PDE+S△PEB-S△EDB,构建二次函数,求出PF的值最大时,点P的坐标为(2$\sqrt{2}$,2$\sqrt{2}$),易知点H的运动轨迹是线段PE的垂直平分线,易知当AH垂直PE的垂直平分线时,AH的值最小.利用相似三角形的性质求出AK,即可解决问题;
(3)如图3中,作MN⊥BD于N.当MN=BD时,存在△MB'D'为等腰直角三角形(只要D′或B′与N重合即可),易知H(0,4$\sqrt{2}$),由△HMN∽△DBE,可得$\frac{MN}{BE}$=$\frac{HM}{BD}$,推出HM=$\frac{50}{9}$$\sqrt{2}$,推出OM=HM-OH=$\frac{50\sqrt{2}}{9}$-4$\sqrt{2}$=$\frac{14}{9}$$\sqrt{2}$,可得M(0,-$\frac{14}{9}$$\sqrt{2}$),点M关于H的对称点M′也满足条件,此时M′(0,$\frac{86\sqrt{2}}{9}$),当M″是HM的中点时,M″是等腰三角形△M″B′D′的直角顶点;
解答 解:(1)如图1中,
对于抛物线y=-$\frac{{\sqrt{2}}}{3}{x^2}+\frac{4}{3}x+2\sqrt{2}$令y=0,得到-$\frac{{\sqrt{2}}}{3}{x^2}+\frac{4}{3}x+2\sqrt{2}$=0,解得x=-$\sqrt{2}$或3$\sqrt{2}$,
∴A(-$\sqrt{2}$,0),B(3$\sqrt{2}$,0),
∵y=-$\frac{{\sqrt{2}}}{3}{x^2}+\frac{4}{3}x+2\sqrt{2}$=-$\frac{\sqrt{2}}{3}$(x-$\sqrt{2}$)2+$\frac{8\sqrt{2}}{3}$.
∴D($\sqrt{2}$,$\frac{8\sqrt{2}}{3}$),
设直线BD的解析式为y=kx+b,则有$\left\{\begin{array}{l}{\sqrt{2}k+b=\frac{8\sqrt{2}}{3}}\\{3\sqrt{2}k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=4\sqrt{2}}\end{array}\right.$,
∴直线BD的解析式为y=-$\frac{4}{3}$x+4$\sqrt{2}$.
(2)如图2中,设P(m,-$\frac{\sqrt{2}}{3}$m2+$\frac{4}{3}$m+2$\sqrt{2}$),连接PD、PB,作PQ⊥OB于Q.
由题意欲求PF的最大值,易知当△PBD面积最大时,PF的值最大,
S△PBD=S△PDE+S△PEB-S△EDB
=$\frac{1}{2}$×$\frac{8\sqrt{2}}{3}$×(m-$\sqrt{2}$)+$\frac{1}{2}$×2$\sqrt{2}$×(-$\frac{\sqrt{2}}{3}$m2+$\frac{4}{3}$m+2$\sqrt{2}$)-$\frac{1}{2}$×2$\sqrt{2}$•$\frac{8\sqrt{2}}{3}$
=-$\frac{2}{3}$(m-2$\sqrt{2}$)2+$\frac{4}{3}$,
∵-$\frac{2}{3}$<0,
∴m=2$\sqrt{2}$时,△PBD的面积最大,PF的值最大,
∴此时P(2$\sqrt{2}$,2$\sqrt{2}$),
易知点H的运动轨迹是线段PE的垂直平分线,
∴当AH垂直PE的垂直平分线时,AH的值最小,设AH交EM于K,
在Rt△EPQ中,PE=$\sqrt{E{Q}^{2}+P{Q}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=$\sqrt{10}$,
由△AKE∽△EQP,得到$\frac{AK}{EQ}$=$\frac{AE}{PE}$,
∴AK=$\frac{2\sqrt{10}}{5}$,易知HK=NE=$\frac{1}{2}$PE=$\frac{\sqrt{10}}{2}$,
∴AH=AK+KH=$\frac{9\sqrt{10}}{10}$.
(3)如图3中,作MN⊥BD于N.
∵B(3$\sqrt{2}$,0),D($\sqrt{2}$,$\frac{8\sqrt{2}}{3}$),
∴BD=$\sqrt{(2\sqrt{2})^{2}+(\frac{8\sqrt{2}}{3})^{2}}$=$\frac{10\sqrt{2}}{3}$,
当MN=BD时,存在△MB'D'为等腰直角三角形(只要D′或B′与N重合即可),
∵直线BD的解析式为y=-$\frac{4}{3}$x+4$\sqrt{2}$,直线BD与y轴的交点H(0,4$\sqrt{2}$),
∵△HMN∽△DBE,
∴$\frac{MN}{BE}$=$\frac{HM}{BD}$,
∴$\frac{\frac{10\sqrt{2}}{3}}{2\sqrt{2}}$=$\frac{HM}{\frac{10\sqrt{2}}{3}}$,
∴HM=$\frac{50}{9}$$\sqrt{2}$,
∴OM=HM-OH=$\frac{50\sqrt{2}}{9}$-4$\sqrt{2}$=$\frac{14}{9}$$\sqrt{2}$,
∴M(0,-$\frac{14}{9}$$\sqrt{2}$),
点M关于H的对称点M′也满足条件,此时M′(0,$\frac{86\sqrt{2}}{9}$),
当M″是HM的中点时,M″是等腰三角形△M″B′D′的直角顶点,此时M″(0,$\frac{11\sqrt{2}}{9}$),
综上所述,满足条件的点M的坐标为(0,-$\frac{14}{9}$$\sqrt{2}$)或(0,$\frac{11}{9}$$\sqrt{2}$)或(0,$\frac{86}{9}$$\sqrt{2}$).
点评 本题考查二次函数综合题、一次函数的应用、垂线段最短、等腰直角三角形的判定和性质、勾股定理.相似三角形的判定和性质等知识,解题的关键是学会构建二次函数解决最值问题,学会用分类讨论的思想思考问题,学会添加常用辅助线解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
 如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的是①②③(填序号).若有错误的结论请改为正确的:CD=BD(若没有请填“无”)
如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的是①②③(填序号).若有错误的结论请改为正确的:CD=BD(若没有请填“无”)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
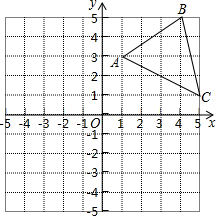 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(1,3),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(1,3),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 气温x/℃ | 0 | 5 | 10 | 15 | 20 |
| 音速y/(m/s) | 331 | 334 | 337 | 340 | 343 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )
某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )| A. | 50米 | B. | 100米 | C. | 125米 | D. | 150米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
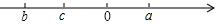 若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )
若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )| A. | a>b>c>0 | B. | c<b<0<a | C. | a>0>c>b | D. | c>b>0>a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m-3 | B. | m+3 | C. | $\frac{m+3}{m-3}$ | D. | $\frac{m-3}{m+3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com