
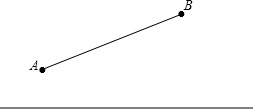
 公路同侧有A、B两个村庄,相距
公路同侧有A、B两个村庄,相距| 17 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,Rt△ABC中∠C=90°,D为AB的中点,分别作AE∥CB、BE∥AC,两线交于点E,连接DE.作EF∥AB交CB延长线于点F,取EF中点G,连接BG.问四边形DEGB是什么特殊四边形?说明理由.
如图,Rt△ABC中∠C=90°,D为AB的中点,分别作AE∥CB、BE∥AC,两线交于点E,连接DE.作EF∥AB交CB延长线于点F,取EF中点G,连接BG.问四边形DEGB是什么特殊四边形?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
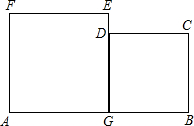 如图所示,这是一块工厂的下脚料铁板,其中AGEF和BCDG都是正方形.某个体水箱加工生产户经过计算得知,这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积(切割,焊接过程中的面积不变),他思考了一会,决定购买这块下脚料用于焊接冰箱.请你利用所学的知识帮助他设计一种最简便的切割,焊接方法,并证明你的设计方案.
如图所示,这是一块工厂的下脚料铁板,其中AGEF和BCDG都是正方形.某个体水箱加工生产户经过计算得知,这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积(切割,焊接过程中的面积不变),他思考了一会,决定购买这块下脚料用于焊接冰箱.请你利用所学的知识帮助他设计一种最简便的切割,焊接方法,并证明你的设计方案.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com