
����Ŀ��ij��˾��![]() ���طֱ������ھ��16̨��12̨�����������ס�������֧Ԯ���裬���м���Ҫ15̨���ҵ���Ҫ13̨.��
���طֱ������ھ��16̨��12̨�����������ס�������֧Ԯ���裬���м���Ҫ15̨���ҵ���Ҫ13̨.��![]() ����һ̨���ס������صķ��÷ֱ���500Ԫ��400Ԫ����
����һ̨���ס������صķ��÷ֱ���500Ԫ��400Ԫ����![]() ����һ̨���ס������ط��÷ֱ���300Ԫ��600Ԫ�����
����һ̨���ס������ط��÷ֱ���300Ԫ��600Ԫ�����![]() ��������
��������![]() ̨�ھ����
̨�ھ����
��1���벹ȫ�±���������������ھ�����ܷ����Ƕ��٣�
�� | �� | �ܼ� | |
|
| ____________̨ | 16̨ |
| _______________̨ | ____________̨ | 12̨ |
�ܼ� | 15̨ | 13̨ | 28̨ |
��2������![]() ��������5̨�ھ��ʱ���������ھ�����ܷ����Ƕ��٣�
��������5̨�ھ��ʱ���������ھ�����ܷ����Ƕ��٣�
��3�������������䷽������ʹ�������ھ�����ܷ������٣����ٷ����Ƕ��٣�
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() Ԫ����2���ܷ�����11100Ԫ����3��
Ԫ����2���ܷ�����11100Ԫ����3��![]() ��������3̨��������13̨��
��������3̨��������13̨��![]() ��������12̨ʱ�����˷����٣������˷�Ϊ��10300Ԫ.
��������12̨ʱ�����˷����٣������˷�Ϊ��10300Ԫ.
��������
��1��ֱ�Ӹ���������ȫ����Ȼ����������ھ�����ܷ���=A�������ķ���+B�������ķ���+A�������ҵķ���+B�������ҵķ��ã���ʽ���㼴�ɣ�
��2����x=5���루1������õ�ʽ�Ӽ��㼴�ɣ�
��3�����ݣ�1�����ܷ��õ�ʽ�ӷ�����x��ֵ�����仯ʱ�ı仯���ɣ����������С����.
�⣺��1����A���ھ��16̨��������x̨��
��A�����ң�16-x��̨��B�����ף�15-x��̨��
��B���ھ��12̨��
��B������12-��15-x��=��x-3��̨��
�ܷ���Ϊ��![]()
![]()
=![]() ��Ԫ����
��Ԫ����
�ʴ��ǣ�![]() ��
��![]() ��
��![]() ��
��![]() Ԫ
Ԫ
��2����![]() ʱ��
ʱ��![]() ��Ԫ����
��Ԫ����
����![]() ��������5̨�ھ��ʱ���������ھ�����ܷ�����11100Ԫ.
��������5̨�ھ��ʱ���������ھ�����ܷ�����11100Ԫ.
��3����Ϊ�ܷ���Ϊ![]() Ԫ������
Ԫ������![]() ԽС�����˷Ѿ�Խ�٣�
ԽС�����˷Ѿ�Խ�٣�
����Ϊ�����̨�������Ǹ���������![]() ��Сȡ3��
��Сȡ3��
��![]() ��������3̨��������13̨��
��������3̨��������13̨��![]() ��������12̨ʱ�����˷����٣�
��������12̨ʱ�����˷����٣�
�����˷�Ϊ��![]() Ԫ.
Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��ֲ֯�������֪�ڼ״�ֲ������220�ˣ����Ҵ�ֲ������96��.
��1����Ҫʹ�״�ֲ�����������Ҵ�ֲ��������3����Ӧ���Ҵ���������ȥ�״�?
��2��Ϊ�˾������ֲ�������ֵ�m��ȥ����֧Ԯ������![]() ����Ҫʹ�״�ֲ����������Ȼ���Ҵ�ֲ��������3������Ӧ�����ף���������������?
����Ҫʹ�״�ֲ����������Ȼ���Ҵ�ֲ��������3������Ӧ�����ף���������������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() ����ֱ��
����ֱ��![]() �ཻ�ڵ�P��2��m������x�ύ�ڵ�A��
�ཻ�ڵ�P��2��m������x�ύ�ڵ�A��
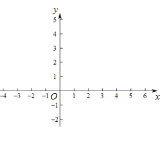
��1����m��ֵ��
��2������P��PB��x����B�������PAB�����Ϊ6����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݲ��ش����⣺
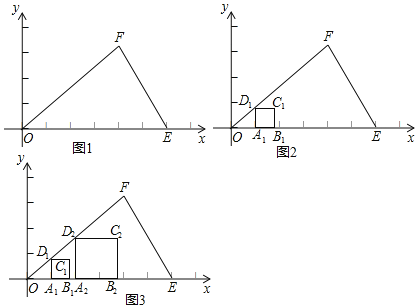
��ͼ1����ƽ��ֱ������ϵxOy�У���һ����OEF��Ҫ���ڡ�OEF����һ���ڽ�������ABCD��ʹ������A��B���������ڡ�OEF��OE���ϣ�����������C��D�ֱ���EF��OF�������ϣ�
С���е�Ҫʹ�ı��ε��ĸ�����ͬʱ��������������Щ���ѣ������������ı��ε��������������������������Ȼ���һ�������������������α��ϵ������Σ���ͼ2�������������ڡ�OEF�ڻ���һ�������������Σ���ͼ3��������������ٶһЩ�����������Σ����ܷ�����Щ��Cλ�õ�����ͼ�Σ��������ͼ�ξ��ܻ��������������������ˣ�
��1������Ҳʵ��һ�£��ٶ���������������Σ�����С��������Щ��C���е�ͼ������ ����
��2������ο�����˼·������������⣺���E��F���������ֱ�ΪE��6��0����F��4��3����
�ٵ�A1�������ǣ�1��0��ʱ����C1���������� ����
�ڵ�A2�������ǣ�2��0��ʱ����C2���������� ����
�۽�ϣ�1���в��룬���������ABCD�Ķ���D�����꣬��ͼ3�л�������������������ABCD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ϵ�»�������![]() ��ͼ��
��ͼ��

��1������������![]() ��ͼ����
��ͼ����![]() ͼ����A��B���㣬A��B����࣬����
ͼ����A��B���㣬A��B����࣬����![]() ��ͼ����A��B��������
��ͼ����A��B��������
��2������ͼ��ֱ��д��![]() ʱ�Ա���x��ȡֵ��Χ
ʱ�Ա���x��ȡֵ��Χ
��3��![]() ��x�ύ��ΪC����
��x�ύ��ΪC����![]() �����
�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
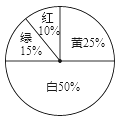
����Ŀ��ij�̳�Ϊ�������˿ͣ�������һ����������ת����ת�̣�����ͼ�������涨������100Ԫ����Ʒ�����ܻ��һ��ת��ת�̵Ļ��ᣬ���ת��ֹͣ��ָ�����ö��졢�̡��ơ���������ô�˿;Ϳ��Էֱ�õ�80Ԫ��30Ԫ��10Ԫ��0Ԫ�Ĺ���ȯ��ƾ����ȯ��Ȼ�������̳��������˿Ͳ�Ը��תת�̣���ô����ֱ�ӻ�ù���ȯ10Ԫ��
��1��ÿת��һ��ת��������ȯ����ƽ�����Ƕ��٣�
��2�����ڴ��̳�����100Ԫ�Ļ����ô�㽫ѡ�����ַ�ʽ��ù���ȯ��
��3��С���ڼ���Ҳ����һ��ͬ����ת����ʵ�飬ת10�κ�ù���ȯ96Ԫ����˵���Dz�תת��ֱ����ȡ����ȯ���㣬��ͬ��С����˵������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
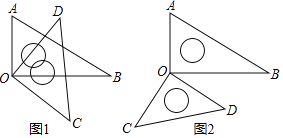
����Ŀ����һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���O����ͼ��ʽ������һ��
��1����ͼ1������BOD��25�㣬���AOC���� ���㣻����AOC��125�㣬���BOD���� ���㣻
��2����ͼ2������BOD��50�㣬���AOC���� ���㣻����AOC��140�㣬���BOD���� ���㣻
��3�������AOC���BOD�Ĵ�С��ϵ���� ���������ͼ��1��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺(![]() )��2��
)��2��![]() +��
+��![]() ��4��0��
��4��0��![]() cos45�㣮
cos45�㣮
���𰸡�1
�������������������ԭʽ�ĵ�һ����ݸ�����ָ���ݵ����廯�ڶ����������ƽ�����Ķ������9������ƽ�����������������ָ����ʽ�������һ����������ǵ����Ǻ���ֵ���ϲ������ֵ.
���������ԭʽ=4��3+1��![]()
=2��1
=1��
�����͡������
��������
16
����Ŀ��������������������������һ�⣺�����ж���ͬ�������������ߣ������������Ҷ��У�������ʮ����б�������һᣮ�ʼ����и���������������˵����֪�ס��Ҷ���ͬʱ��ͬһ��
����������ٶ�Ϊ7���ҵ��ٶ�Ϊ3����һֱ���ߣ�����������10��������б��ƫ����������һ�κ�������������ô����ʱ�������Ҹ����˶�Զ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Կ�չ��ѧ��ÿ�����1Сʱ���������ij��ѧ����ѧУʵ���������������A����ӣ�B������C���ܲ���D�����������˶���Ŀ��Ϊ���˽�ѧ����ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼͳ��ͼ������ͼ����Ϣ����������⣺
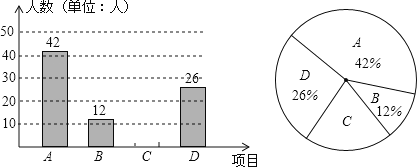
��1����У���ε����У��������˶�����ѧ����
��2���뽫����ͳ��ͼ����������
��3���ڱ��ε����ѧ���������ȡ1�ˣ���ϲ�����ܲ����ĸ����ж��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com