
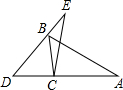
 如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△EDC≌△ABC,则∠BCE:∠BCD=1:4.
如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△EDC≌△ABC,则∠BCE:∠BCD=1:4. 分析 先求出△ABC的各角的度数,再根据全等三角形对应角相等求出∠ECD的度数,利用邻补角的定义先求出∠ECA的度数,根据∠BCE=∠ACB-∠ECA求出∠BCE的度数,然后求出比值.
解答 解:∵∠A:∠ABC:∠ACB=3:5:10,
∴∠ACB=180°×$\frac{10}{3+5+10}$=100°,
∵△EDC≌△ABC,
∴∠ECD=∠ACB=100°,
∴∠ECA=180°-∠ECD=180°-100°=80°,
∠BCE=∠ACB-∠ECA=100°-80°=20°,
∴∠BCD=80°
∴∠BCE:∠BCD=20°:80°=1:4.
故答案为1:4.
点评 本题主要考查全等三角形对应角相等的性质和邻补角之和等于180°,根据比值和三角形内角和定理求出∠ACB的度数是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
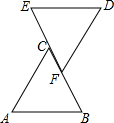 如图,已知EC=BF,∠A=∠D,现从下列6个条件:
如图,已知EC=BF,∠A=∠D,现从下列6个条件:| A. | ②③④⑥ | B. | ③④⑤⑥ | C. | ①③④⑥ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
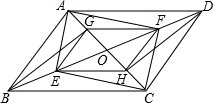 如图,在?ABCD中,AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,BG⊥AC于点G,DH⊥AC于点H,连接EH、HF、FG、GE,那么四边形EHFG是平行四边形吗?请说明理由.
如图,在?ABCD中,AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,BG⊥AC于点G,DH⊥AC于点H,连接EH、HF、FG、GE,那么四边形EHFG是平行四边形吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com