
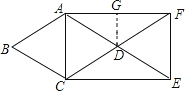
【题目】如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
A.四边形ACEF是平行四边形,它的周长是4
B.四边形ACEF是矩形,它的周长是2+2![]()
C.四边形ACEF是平行四边形,它的周长是4![]()
D.四边形ACEF是矩形,它的周长是4+4![]()
【答案】B
【解析】解:∵DE=AD,DF=CD,
∴四边形ACEF是平行四边形,
∵四边形ABCD为菱形,
∴AD=CD,
∴AE=CF,
∴四边形ACEF是矩形,
∵△ACD是等边三角形,
∴AC=1,
∴EF=AC=1,
过点D作DG⊥AF于点G,则AG=FG=AD×cos30°=![]() ,
,
∴AF=CE=2AG=![]() ,
,
∴四边形ACEF的周长为:AC+CE+EF+AF=1+![]() +1+
+1+![]() =2+2
=2+2![]() ,
,
故选B.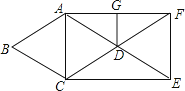
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】在ABCD中,AB<BC,已知∠B=30°,AB=![]() ,将△ABC沿AC翻折至△AB′C,使点B′落在ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为 .
,将△ABC沿AC翻折至△AB′C,使点B′落在ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1<y2 ,
,y2)为函数图象上的两点,则y1<y2 ,
其中正确结论是( )
A.②④
B.①④
C.①③
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某苹果生产基地,用30名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4000元;加工成罐头出售每吨获利10000元.采摘的工人每人可以采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式.
(2)如何分配工人才能获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A、B两种品牌的龟苓膏共1000包.
(1)若小王按需购买A、B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式.
(3)在2中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本(运算结果取整数)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.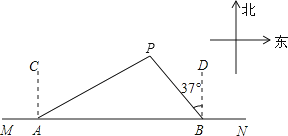
(1)尺规作图:过点P作AB所在直线的垂线,垂足为E(要求:保留作图痕迹,不写作法);
(2)求船P到海岸线MN的距离(即PE的长);
(3)若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,F为BC边上的中点,连接AF交对角线BD于G,在BD上截BE=BA,连接AE,将△ADE沿AD翻折得△ADE′,连接E′C交BD于H,若BG=2,则四边形AGHE′的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2 , 且x12+x22﹣x1x2=7,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com