
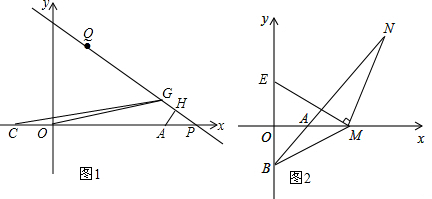
分析 (1)根据非负数是性质:几个非负数的和为零,这几个非负数为零,即可解决.
(2)如图1中,连接AE、EN,作NF⊥OA于F,思想利用四点共圆证明△EMN是等腰直角三角形,再证明△EMO≌△MNF得NF=MO,MF=EO=12,设点M(m,0),列出方程解决.
(3)∠CGQ的大小不变,如图2中,连接QA、QC,过C作CT⊥PQ于T,过Q作QS⊥x轴于点S,先证明△CQT≌△QAH,再证明△TCG是等腰直角三角形即可.
解答 解:(1)∵$\sqrt{a-12}$+(a+b)2+(c+4)2=0,
$\sqrt{a-12}$≥0,(a+b)2≥0,(c+4)2≥0,
∴a=12,b=-12,c=-4.
(2)如图1中,连接AE、EN,作NF⊥OA于F.
∵OA=OE=OB=12,∠EOA=∠AOB=90°,
∴∠EAO=∠AEO=∠OAB=∠OBA=45°,
∴∠EAB=∠EAN=90°,
∵∠EAN=∠EMN=90°,
∴四边形EAMN四点共圆,
∴∠EAO=∠ENM=45°,
∴∠MEN=∠MNE=45°,
∴EM=MN,
∵∠EMO+∠NMF=90°,∠NMF+∠MNF=90°,
∴∠EMO=∠MNF,
在△EMO和△MNF中,
$\left\{\begin{array}{l}{∠EOM=∠MFN}\\{∠EMO=∠MNF}\\{EM=MN}\end{array}\right.$,
∴△EMO≌△MNF,
∴NF=MO,MF=EO=12,设点M(m,0),
∵S△AMN=$\frac{3}{2}$S△AMB
∴$\frac{1}{2}$×(m-12)×m=$\frac{3}{2}$×$\frac{1}{2}$×(m-12)×12,
∴m=18,
∴点M坐标为(18,0)
(3)∠CGQ的大小不变不改变,理由如下:
如图2中,连接QA、QC,过C作CT⊥PQ于T,过Q作QS⊥x轴于点S,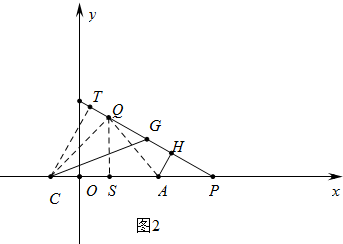 ∵Q(4,8),C(-4,0),A(12,0),
∵Q(4,8),C(-4,0),A(12,0),
∴S(4,0),
∴MS垂直平分AC,
∴QC=QA8,
∴QS=AS=SC,
∴∠CQA=90°,
∴∠CQT+∠QMH=∠TCQ+∠CQT=90°,
∴∠TCQ=∠AQH,
在△CMT和△MAH中
$\left\{\begin{array}{l}{∠CTQ=∠QHA=90°}\\{∠TCQ=∠AQH}\\{CQ=QA}\end{array}\right.$,
∴△CQT≌△QAH(AAS),
∴TQ=AH,CT=QH,
又AH=HG,
∴QT=GH=AH,
∴GT=GQ+QT=QG+GH=QH=CT,
∴△CGT是等腰直角三角形,
∴∠CGQ=45°,
即当点P在点A右侧运动时,∠CGQ的度数不改变.
点评 本题考查等腰三角形的性质、全等三角形的判定和性质、四点共圆等知识,解题的关键是添加辅助线构造全等三角形,利用特殊三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
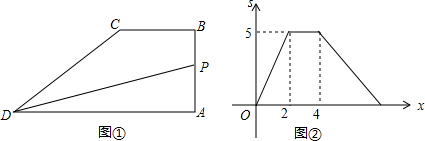
| A. | 4 | B. | 2+$\sqrt{13}$ | C. | 5 | D. | 4+$\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$ | B. | $\sqrt{12}$ | C. | $\sqrt{30}$ | D. | $\sqrt{\frac{1}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com