
 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1.
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1.分析 (1)由等边三角形的性质可知AB=AC,∠BAC=∠C=60°.依据SAS可证明△ABE≌△CAD,依据全等三角形的性质可得到∠ABE=∠CAD,最后结合三角形的外角的性质求解即可;
(2)先求得∠PBQ=30°,然后依据含30度直角三角形的性质可求得BP=8,故此可求得BE=9,最后依据全等三角形的性质可得到AD=BE=9
解答 解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°.
∵在△ABE和△CAD中$\left\{\begin{array}{l}{DC=AE}\\{∠C=∠BAE}\\{AC=AB}\end{array}\right.$,
∴△ABE≌△CAD.
∴∠ABE=∠CAD.
∵∠BPQ是△ABP的一个外角,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.
(2)解:∵BQ⊥AD,∴∠AQB=90°.
又由(1)知,∠BPQ=60°,
∴∠PBQ=30°.
∴BP=2PQ=2×4=8.
∴BE=BP+PE=8+1=9.
又∵由(1)知△ABE≌△CAD,
∴AD=BE=9.
点评 本题主要考查的是全等三角形的性质和判定、等边三角形的性质、含30°直角三角形的性质,熟练掌握全等三角形的判定定理、等边三角形的性质、含30°直角三角形的性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
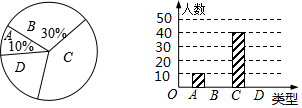 某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.
某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠AOB=90°,射线OM平分∠AOC,ON平分∠BOC.
如图,∠AOB=90°,射线OM平分∠AOC,ON平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com