
���� ��1�������ʵ����⣬�ý������������ģ�ͽ��
��2���������ֳ�λ������δ֪����������ʽ�Ͳ���ʽ���ֹ�ϵ������λ��Ϊ��������������Ϊ���⣮����Ҳ�ͳ����ˣ�
��� �⣺��1�����ͥ�γ�ӵ��������ƽ��������Ϊx��
��64��1+x��2=100��
���x=0.25=25%��x=-2.25���������⣬��ȥ����
��100��1+25%��=125��
�𣺸�С����2013���ͥ�γ����ﵽ125����
��2�����С���ɽ����ڳ�λa����¶�쳵λb����
��$\left\{\begin{array}{l}{5a+b=150}\\{2a��b��2.5a}\end{array}\right.$��
�ɢٵ�b=150-5a��
����ڵ�20��a��$\frac{150}{7}$��
��a����������
��a=20��21��
��a=20ʱb=50����a=21ʱb=45��
���һ�������ڳ�λ20����¶�쳵λ50����
�����������ڳ�λ21����¶�쳵λ45��
���� ���⿼����һԪ���η��̼�һԪһ�β���ʽ��Ӧ�ã�����ۺ��⣬��Ҫ��dz���������⣬�������⣬������δ֪�����ֲ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 1-2$\sqrt{3}$ | C�� | 3-2$\sqrt{3}$ | D�� | 2$\sqrt{3}$-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=2��BC=2$\sqrt{3}$��DΪ�߶�AC��һ�㣬��DEF�DZ߳�Ϊa��aΪС��2$\sqrt{3}$�ij������ĵȱ������Σ���DE��AB������DEF��AC��������ƽ�ƣ����DEF���ABC�ص����ֵ��ܳ�ΪL��
��ͼ����Rt��ABC�У���ACB=90�㣬AC=2��BC=2$\sqrt{3}$��DΪ�߶�AC��һ�㣬��DEF�DZ߳�Ϊa��aΪС��2$\sqrt{3}$�ij������ĵȱ������Σ���DE��AB������DEF��AC��������ƽ�ƣ����DEF���ABC�ص����ֵ��ܳ�ΪL���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
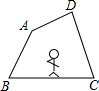 ��ͼ��С���ػ��ڵ����ϵ��ı���ABCD�ı���ʱ����һȦ�ص�ԭ�أ�
��ͼ��С���ػ��ڵ����ϵ��ı���ABCD�ı���ʱ����һȦ�ص�ԭ�أ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
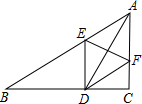 ��ͼ����ABC�У���C=90�㣬ADƽ�֡�BAC��ED��BC��DF��AB����֤��AD��EF���ഹֱƽ�֣�
��ͼ����ABC�У���C=90�㣬ADƽ�֡�BAC��ED��BC��DF��AB����֤��AD��EF���ഹֱƽ�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com