Question

19．如图，在Rt△ABC中，∠ACB=90°，AC=2，BC=2$\sqrt{3}$，D为线段AC上一点，△DEF是边长为a（a为小于2$\sqrt{3}$的常数）的等边三角形，且DE∥AB，将△DEF沿AC方向上下平移，设△DEF与△ABC重叠部分的周长为L．
（1）在△DEF沿AC方向上下平移过程中E到AC的距离是否发生变化？为什么？
（2）若AD=$\frac{1}{2}$，当a=2时，求L的值；
（3）若点D运动到AC的中点处，请用含a的代数式表示L．

Answer 1

分析 （1）先作出点E到AC的距离EH，根据三角函数求出∠A的度数，再由平行线求∠CDE的度数，利用三角函数列等式表示EH的长为$\frac{\sqrt{3}}{2}$a，因为a是一个常数，所以E到AC的距离是一个常数，不发生变化；
（2）如图2，作辅助线，构建平行四边形，证明四边形ADGM和四边形MGEN是平行四边形，再证明△ADM和△DMG是等边三角形，依次求出重叠部分各边的长：MN、DM、EN的长，最后相加即可；
（3）先计算△DEF在特殊位置时对应的边长a的值：i）如图3，当点F恰好在AB上时，a=1，ii）如图4，当点E恰好在BC边上时，a=2，
所以分三种情况讨论：①当0＜a≤1时，如图5，△DEF在△ABC的内部，重叠部分周长就是△DEF的周长，L=3a；
②当1＜a≤2时，如图6，类似图2作辅助线，得DG=DM=AD=EN=1，则MN=EG=a-1，表示出重叠部分周长L；
③当2＜a＜2$\sqrt{3}$，如图7，点E和F都在△ABC的外部，在Rt△PDC中，分别计算出PQ、QE、PE的长，L可以表示为四边形MDEN的周长-EQ-PE+PQ，代入可求得．

解答 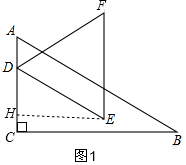解：（1）如图1，E到AC的距离不发生变化，理由是：
过E作EH⊥AC于H，
由题意得：tan∠A=$\frac{BC}{AC}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$，
∴∠A=60°，
∵DE∥AB，
∴∠CDE=∠A=60°，
∴sin∠CDE=$\frac{EH}{DE}$，
∴EH=sin60°•a=$\frac{\sqrt{3}}{2}$a，
∴E到AC的距离是一个常数，不发生变化；
（2）如图2，过M作MG∥AC，交DE于G，
∵△DEF是等边三角形，
∴∠MDE=60°，
由（1）得：∠CDE=60°，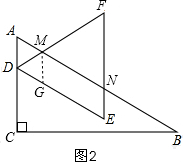
∴∠ADM=180°-60°-60°=60°，
∵∠A=60°，
∴△ADM是等边三角形，
∴DM=AD=$\frac{1}{2}$，
∵AM∥DG，AD∥MG，
∴四边形ADGM是平行四边形，
∴∠DGM=∠A=60°，
∴△DMG是等边三角形，
∴DG=DM=$\frac{1}{2}$，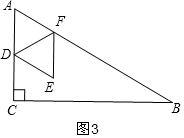
∴GE=2-DG=2-$\frac{1}{2}$=$\frac{3}{2}$，
∵∠MGD=∠E=60°，
∴MG∥EF，
∴四边形MGEN是平行四边形，
∴NE=MG=$\frac{1}{2}$，MN=MG=$\frac{3}{2}$，
∴L=MN+DM+DE+EN，
=$\frac{3}{2}$+$\frac{1}{2}$+$\frac{1}{2}$+2，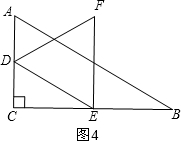
=$\frac{9}{2}$；
（3）如图3，当点F恰好在AB上时，
∵D运动到AC的中点，
∴AD=$\frac{1}{2}$AC=1，
由（2）得：DE=AD=1，即此时a=1，
如图4，当点E恰好在BC边上时，
∵D运动到AC的中点，DE∥AB，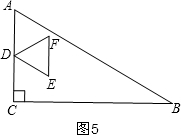
∴E是BC的中点，
∴DE=$\frac{1}{2}$AB，
在Rt△ABC中，∵AC=2，∠B=30°，
∴AB=4，
∴DE=2，即此时a=2，
所以若点D运动到AC的中点处时，分三种情况讨论：
①当0＜a≤1时，如图5，△DEF在△ABC的内部，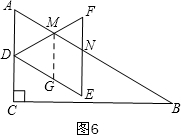
∴L=3a，
②当1＜a≤2时，如图6，点E在△ABC的内部，点F在△ABC的外部，
过M作MG∥EF，交DE于G，
由（2）同理得：DG=DM=AD=EN=1，
∴MN=EG=a-1，
∴L=MN+DM+EN+DE=a-1+1+1+a=2a+1；
③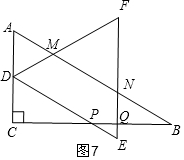当2＜a＜2$\sqrt{3}$，如图7，点E和F都在△ABC的外部，
在Rt△PDC中，∵CD=1，∠CDP=60°，
tan∠CDP=$\frac{PC}{DC}$，
∴PC=1×tan60°=$\sqrt{3}$，
由（1）得：点E到AC的距离为$\frac{\sqrt{3}}{2}$a，
∴PQ=$\frac{\sqrt{3}}{2}$a-PC=$\frac{\sqrt{3}}{2}$a-$\sqrt{3}$，
tan30°=$\frac{QE}{PQ}$，
∴QE=PQ•tan30°=（$\frac{\sqrt{3}}{2}$a-$\sqrt{3}$）•$\frac{\sqrt{3}}{3}$=$\frac{1}{2}$a-1，
∴PE=2QE=a-2，
由②得：四边形MDEN的周长=2a+1，
∴L=四边形MDEN的周长-EQ-PE+PQ=2a+1-（$\frac{1}{2}$a-1）-（a-2）+$\frac{\sqrt{3}}{2}$a-$\sqrt{3}$=$\frac{\sqrt{3}+1}{2}$a+4-$\sqrt{3}$；
综上所述：若点D运动到AC的中点处，L的关系式为：
L=$\left\{\begin{array}{l}{3a（0＜a≤1）}\\{2a+1（1＜a≤2）}\\{\frac{\sqrt{3}+1}{2}a+4-\sqrt{3}（2＜a＜2\sqrt{3}）}\end{array}\right.$．

点评 本题是几何变换的综合题，考查了等边三角形、30°角的直角三角形的性质，利用了特殊角的三角函数值列式求线段的长；熟练掌握等边三角形的各边相等，且每个角都等于60°，知道等边三角形常用的判定方法：有一个角是60°的等腰三角形是等边三角形；同时还考查了平行四边形的判定和性质，利用对边相等求线段的长，最后利用周长公式求出重叠部分的周长L．