
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| 9x2-2=0 | $\frac{\sqrt{2}}{3}$ | -$\frac{\sqrt{2}}{3}$ | 0 | |
| 2x2-3x=0 | 0 | $\frac{3}{2}$ | $\frac{3}{2}$ | 0 |
| x2-3x+2=0 | 1 | 2 | 3 | 2 |
| 关于x的方程ax2+bx+c=0(a≠0,b2-4ac≥0) | $\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$ | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ |
分析 (1)根据表中给出的x1、x2的值,分别进行计算即可得出答案,从而补全统计表;
(2)根据(1)中的第四行的结论,推广到一般进行总结;
(3)根据(2)得出的 x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,求出x1+x2和x1•x2的值,再把要求的式子进行整理,然后代值计算即可得出答案.
解答 解:(1)∵x1=$\frac{\sqrt{2}}{3}$,x2=-$\frac{\sqrt{2}}{3}$,
∴x1•x2=-$\frac{2}{9}$,
∵x1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,x2=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$,
∴x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$;
填表如下:
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| 9x2-2=0 | $\frac{\sqrt{2}}{3}$ | -$\frac{\sqrt{2}}{3}$ | 0 | -$\frac{2}{9}$ |
| 2x2-3x=0 | 0 | $\frac{3}{2}$ | $\frac{3}{2}$ | 0 |
| x2-3x+2=0 | 1 | 2 | 3 | 2 |
| 关于x的方程ax2+bx+c=0(a≠0,b2-4ac≥0) | $\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$ | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ | -$\frac{b}{a}$ | $\frac{c}{a}$ |
点评 此题考查了根与系数的关系,熟悉一元二次方程根与系数的关系的猜想过程与证明过程是本题的关键.


科目:初中数学 来源: 题型:选择题
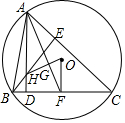 如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )
如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )| A. | 2:4 | B. | 1:3 | C. | 2:5 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D为线段AC上一点,△DEF是边长为a(a为小于2$\sqrt{3}$的常数)的等边三角形,且DE∥AB,将△DEF沿AC方向上下平移,设△DEF与△ABC重叠部分的周长为L.
如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D为线段AC上一点,△DEF是边长为a(a为小于2$\sqrt{3}$的常数)的等边三角形,且DE∥AB,将△DEF沿AC方向上下平移,设△DEF与△ABC重叠部分的周长为L.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
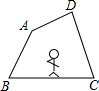 如图,小明沿画在地面上的四边形ABCD的边逆时针走一圈回到原地.
如图,小明沿画在地面上的四边形ABCD的边逆时针走一圈回到原地.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com