
【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
【答案】![]()
【解析】试题解析:∵二次函数有最小值﹣2,
∴y=﹣![]() ,
,
解得:m=![]() .
.
【题型】填空题
【结束】
19
【题目】如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)

(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
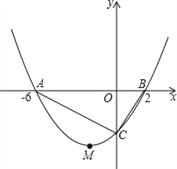
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )

A. π-4 B. ![]() π-1 C. π-2 D.
π-1 C. π-2 D. ![]() -2
-2
【答案】C
【解析】试题解析:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴△OBC的BC边上的高为:![]() OB=
OB=![]() ,
,
∴BC=2![]()
∴S阴影=S扇形OBC﹣S△OBC=![]() .
.
故选C.
【题型】单选题
【结束】
10
【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.

【答案】M、N两点之间的直线距离为1500米.
【解析】试题分析:先根据相似三角形的判定得出△ABC∽△AMN,再利用相似三角形的性质解答即可.
试题解析:在△ABC与△AMN中, ![]() ,
, ![]() =
=![]() ,∴
,∴![]() ,又∵∠A=∠A,
,又∵∠A=∠A,
∴△ABC∽△AMN,∴![]() ,即
,即![]() ,
,
解得:MN=1500米,
答:M、N两点之间的直线距离是1500米;
考点:相似三角形的应用.
【题型】解答题
【结束】
23
【题目】如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C, ![]() .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在北偏东65°45′的方向上,渔船向正东方向航行l小时45分钟之后到达D点,观测到灯塔B恰好在正北方向上,已知两个灯塔之间的距离是12海里,渔船的速度是16海里/时,又知在灯塔C周围18.6海里内有暗礁,问这条渔船按原来的方向继续航行,有没有触礁的危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )

A. ②③④ B. ①②③ C. ②③ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com