
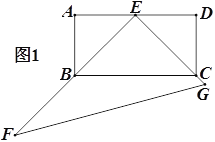
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
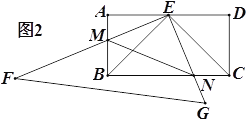
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
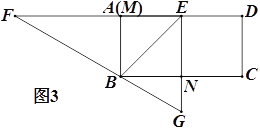
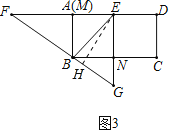
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.
【答案】(1)详见解析;(2)①详见解析;②2;③![]() .
.
【解析】
(1)只要证明△BAE≌△CDE即可;
(2)①利用(1)可知△EBC是等腰直角三角形,根据ASA即可证明;
②构建二次函数,利用二次函数的性质即可解决问题;
③如图3中,作EH⊥BG于H.设NG=m,则BG=2m,BN=EN=![]() m,EB=
m,EB=![]() m.利用面积法求出EH,根据三角函数的定义即可解决问题.
m.利用面积法求出EH,根据三角函数的定义即可解决问题.
(1)证明:如图1中,
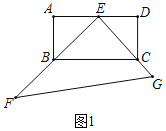
∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵E是AD中点,
∴AE=DE,
∴△BAE≌△CDE,
∴BE=CE.
(2)①解:如图2中,

由(1)可知,△EBC是等腰直角三角形,
∴∠EBC=∠ECB=45°,
∵∠ABC=∠BCD=90°,
∴∠EBM=∠ECN=45°,
∵∠MEN=∠BEC=90°,
∴∠BEM=∠CEN,
∵EB=EC,
∴△BEM≌△CEN;
②∵△BEM≌△CEN,
∴BM=CN,设BM=CN=x,则BN=4-x,
∴S△BMN=![]() x(4-x)=-
x(4-x)=-![]() (x-2)2+2,
(x-2)2+2,
∵-![]() <0,
<0,
∴x=2时,△BMN的面积最大,最大值为2.
③解:如图3中,作EH⊥BG于H.设NG=m,则BG=2m,BN=EN=![]() m,EB=
m,EB=![]() m.
m.
∴EG=m+![]() m=(1+
m=(1+![]() )m,
)m,
∵S△BEG=![]() EGBN=
EGBN=![]() BGEH,
BGEH,
∴EH=![]() =
=![]() m,
m,
在Rt△EBH中,sin∠EBH=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,![]() 的最小值为0;
的最小值为0;![]() .当
.当![]() 时有
时有![]() ;且对于任意实数
;且对于任意实数![]() ,
,![]() .
.
(1)![]() 的对称轴为_________,顶点坐标为_____________;
的对称轴为_________,顶点坐标为_____________;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)令![]() ,试求实数
,试求实数![]() ,使得实数
,使得实数![]() 最大,当
最大,当![]() 时
时![]() 成立.
成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为![]() ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面![]() 高为8米的点
高为8米的点![]() 、
、![]() 处要安装两盏警示灯,则这两盏灯的水平距离
处要安装两盏警示灯,则这两盏灯的水平距离![]() 是____米.
是____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四 边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在X轴上,直线BD交Y轴于点F,交OE于点H,线段BC、OC的长是方程x2-6x+8=0的两个根,且OC>BC.
(1)求直线BD的解析式.
(2)求 △OFH的面积.
(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且
,且![]() .
.
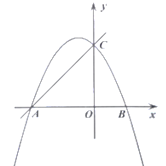
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为第一象限内的一点,当
为第一象限内的一点,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,连接
为斜边的等腰直角三角形时,连接![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并写出自变量
,并写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,连接![]() 、
、![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置(
的位置(![]() 与
与![]() 对应),若
对应),若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,取格点A、B、C并连接AB,BC.取格点D、E并连接,交AB于点F.
(Ⅰ)AB的长等于_____;
(Ⅱ)若点G在线段BC上,且满足AF+CG=FG,请在如图所示的网格中,用无刻度的直尺,确定点G的位置,并简要说明点G的位置是如何找到的.

查看答案和解析>>
科目:初中数学 来源: 题型:
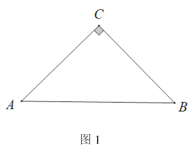
【题目】(1)如图1,△ABC 中,AC=BC,∠ACB=90°.请用直角三角尺(仅可画直角或直线)在图中画出一个点P,使得∠APB=45°;
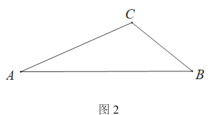
(2)如图2,△ABC 中,AB=a,∠ACB=![]() ,请用直尺和圆规作出一个点Q,使点Q与点C在AB同侧,QA=QB,∠AQB=
,请用直尺和圆规作出一个点Q,使点Q与点C在AB同侧,QA=QB,∠AQB=![]() ;(不写作法,保留作图痕迹)
;(不写作法,保留作图痕迹)
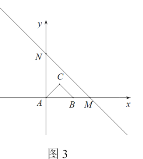
(3)如图3,若 AC=BC=![]() ,∠ACB=90°,以点A为原点,直线AB 为 x 轴,过点A垂直于AB的直线为 y 轴,建立平面直角坐标系,直线y= - x+b(b>0)交 x 轴于点M,交 y 轴于点N.当点P在直线MN上,且∠APB=45°,求点P的个数及对应的b的取值范围;
,∠ACB=90°,以点A为原点,直线AB 为 x 轴,过点A垂直于AB的直线为 y 轴,建立平面直角坐标系,直线y= - x+b(b>0)交 x 轴于点M,交 y 轴于点N.当点P在直线MN上,且∠APB=45°,求点P的个数及对应的b的取值范围;
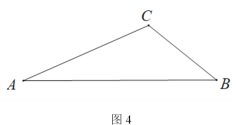
(4)如图4,△ABC 中,AB=a,∠ACB=![]() ,请用直尺和圆规作出点P,使得∠APB=
,请用直尺和圆规作出点P,使得∠APB=![]() 且AP+BP最大,请简要说明理由.(不写作法,保留作图痕迹)
且AP+BP最大,请简要说明理由.(不写作法,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() ,回答下列问题:
,回答下列问题:
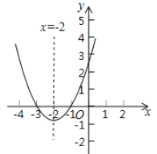
(1)求出此抛物线的对称轴和顶点坐标;
(2)写出抛物线与![]() 轴交点
轴交点![]() 、
、![]() 的坐标,与
的坐标,与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
(3)写出函数的最值和增减性;
(4)![]() 取何值时,①
取何值时,①![]() ,②
,②![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com