
如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0),将矩形OABC绕点O按顺时针方向旋转1350,得到矩形EFGH(点E与O重合).
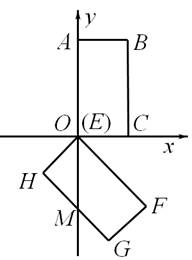
(1)若GH交y轴于点M,则∠FOM= ,OM= ;
(2)矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFHG与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤ 时,S与t之间的函数关系式.
时,S与t之间的函数关系式.
(1)450, ;(2)①
;(2)① -2;②
-2;② .
.
【解析】
试题分析:(1)由旋转的性质,得∠AOF=1350,∴∠FOM=450,由旋转的性质,得∠OHM=450,OH=OC=2,∴OM= ;(2)①由矩形的性质和已知AD∥BO,可得四边形ABOD是平行四边形,从而DO=AB=2,又由△DOI是等腰直角三角形可得OI=OD=2,从而由平移的性质可求得t=IM=OM-OI=
;(2)①由矩形的性质和已知AD∥BO,可得四边形ABOD是平行四边形,从而DO=AB=2,又由△DOI是等腰直角三角形可得OI=OD=2,从而由平移的性质可求得t=IM=OM-OI= -2;②首先确定当0<t≤
-2;②首先确定当0<t≤ 时,矩形EFGH沿y轴向上平移过程中关键点的位置,分0<t≤2,2<t≤
时,矩形EFGH沿y轴向上平移过程中关键点的位置,分0<t≤2,2<t≤ ,
, <t≤
<t≤ 三种情况求出S与t之间的函数关系式.
三种情况求出S与t之间的函数关系式.
试题解析:(1)450; .
.
(2)①如图1,设直线HG与y轴交于点I,
∵四边形OABC是矩形,∴AB∥DO,AB=OC.
∵C(2,0),∴AB=OC=2.
又∵AD∥BO, ∴四边形ABOD是平行四边形. ∴DO=AB=2.
由(1)易得,△DOI是等腰直角三角形,∴OI=OD=2.
∴t=IM=OM-OI= -2.
-2.

②如图2,

过点F,G分别作x轴,y轴的垂线,垂足为R,T,连接OC. 则
由旋转的性质,得,OF=OA=4,∠FOR=450,
∴OR=RF= ,F(
,F( ,-
,- ).
).
由旋转的性质和勾股定理,得OG= ,
,
设TG=MT=x,则OT=OM+MT= .
.
在Rt△OTG中,由勾股定理,得 ,解得x=
,解得x= .
∴G(
.
∴G( ,-
,- ).
).
∴用待定系数法求得直线FG的解析式为 .
.
当x=2时, .
.
∴当t= 时,就是GF平移到过点C时的位置(如图5).
时,就是GF平移到过点C时的位置(如图5).
∴当0<t≤ 时,几个关键点如图3,4,5所示:
时,几个关键点如图3,4,5所示:
如图3 ,t=OE=OC=2,此时,矩形EFGH沿y轴向上平移过程中边EF经过点C;

如图4,t=OE=OM= ,此时,矩形EFGH沿y轴向上平移过程中边HG经过点O;
,此时,矩形EFGH沿y轴向上平移过程中边HG经过点O;

如图5,t=OE= ,此时,矩形EFGH沿y轴向上平移过程中边FG经过点C.
,此时,矩形EFGH沿y轴向上平移过程中边FG经过点C.

∴(Ⅰ)当0<t≤2时,矩形EFHG与矩形OABC重叠部分的面积为△OCS的面积(如图6).此时,OE=OS= t, ∴ .
.

(Ⅱ)当2<t≤ 时,矩形EFHG与矩形OABC重叠部分的面积为直角梯形OEPC的面积(如图7).此时OE= t,,OC=2.
时,矩形EFHG与矩形OABC重叠部分的面积为直角梯形OEPC的面积(如图7).此时OE= t,,OC=2.

由E(0,t),∠FFO=450,用用待定系数法求得直线EP的解析式为 .
.
当x=2时, . ∴CP=
. ∴CP= .
∴
.
∴ .
.
(Ⅲ)当 <t≤
<t≤ 时,矩形EFHG与矩形OABC重叠部分的面积为五边形EQCUV的面积(如图8),
时,矩形EFHG与矩形OABC重叠部分的面积为五边形EQCUV的面积(如图8),

它等于直角梯形EQCO的面积减去直角三角形VOU的的面积.
此时,OE= t,,OC=2,CQ=  ,OU=OV= t-
,OU=OV= t- .
.
∴ .
.
综上所述,当0<t≤ 时,S与t之间的函数关系式为
时,S与t之间的函数关系式为 .
.
考点:1.旋转的性质;2.矩形的性质;3.勾股定理;4.平移的性质;5.平行四边形的判定和性质;6.等腰直角三角形的判定和性质;7.待定系数法;8.直线上点的坐标与方程的关系;9.分类思想的应用.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
 如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足|OA-2|+(OC-2
如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足|OA-2|+(OC-2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
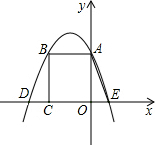 如图,矩形OABC在平面直角坐标系中的位置如图所示,OA=3,AB=2.抛物线y=ax2+bx+c(a≠0)经过点A和点B,与x轴分别交于点D、E(点D在点E左侧),且OE=1,则下列结论:
如图,矩形OABC在平面直角坐标系中的位置如图所示,OA=3,AB=2.抛物线y=ax2+bx+c(a≠0)经过点A和点B,与x轴分别交于点D、E(点D在点E左侧),且OE=1,则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:
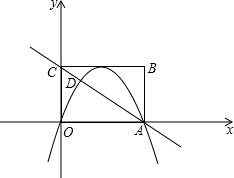 (2013•昆明)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
(2013•昆明)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
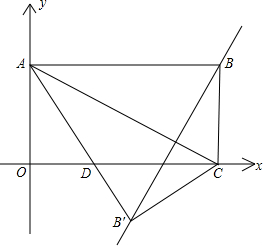
 (2012•浙江二模)如图,矩形OABC在平面直角坐标系中,A(0,3),C(4,0),点P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90°交直线BC于点Q,当△POQ为等腰三角形时,点P坐标为
(2012•浙江二模)如图,矩形OABC在平面直角坐标系中,A(0,3),C(4,0),点P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90°交直线BC于点Q,当△POQ为等腰三角形时,点P坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
 按顺时针方向旋转135°,得到矩形EFGH(点E与O重合).
按顺时针方向旋转135°,得到矩形EFGH(点E与O重合).| 2 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com