
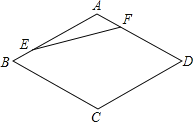
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点E、F分别在边AB、AD上且AE=DF,则△AEF面积的最大值为_____.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】“分组合作学习”成为我市推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
分组前学生学习兴趣 分组后学生学习兴趣
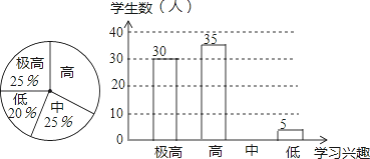
请结合图中信息解答下列问题:
(1)求出分组前学生学习兴趣为“高”的所占的百分比为 ;
(2)补全分组后学生学习兴趣的统计图;
(3)通过“分组合作学习”前后对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
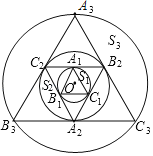
【题目】如图,小圆O的半径为1,△A1B1C1,△A2B2C2,△A3B3C3,…,△AnBnn依次为同心圆O的内接正三角形和外切正三角形,由弦A1C1和弧A1C1围成的弓形面积记为S1,由弦A2C2和弧A2C2围成的弓形面积记为S2,…,以此下去,由弦Ann和弧Ann围成的弓形面积记为Sn,其中S2020的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是直径AB所对的半圆弧,点C在
是直径AB所对的半圆弧,点C在![]() 上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
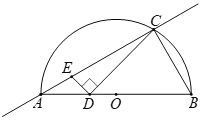
小明根据学习函数的经验,对线段AE,AD长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点D在AB上的不同位置,画图、测量,得到线段AE,AD长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | ||
AE/cm | 0.00 | 0.41 | 0.77 | 1.00 | 1.15 | 1.00 | 0.00 | 1.00 | 4.04 | … |
AD/cm | 0.00 | 0.50 | 1.00 | 1.41 | 2.00 | 2.45 | td style="width:10%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">3.21 | 3.50 | … |
在AE,AD的长度这两个量中,确定_______的长度是自变量,________的长度是这个自变量的函数;
(2)在下面的平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
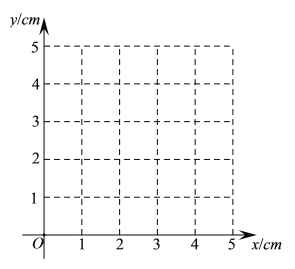
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为________cm(结果精确到0.1).
AD时,AD的长度约为________cm(结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数关系式;
(2)若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,
FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )

A.1∶3 B.2∶3 C.![]() ∶2 D.
∶2 D.![]() ∶3
∶3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种进价为每件40元的商品,通过调查发现,当销售单价在40元至65元之间(![]() )时,每月的销售量
)时,每月的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.
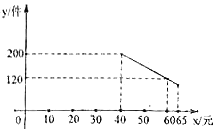
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设每月获得的利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若想每月获得1600元的利润,那么销售单价应定为多少元?
(4)当销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为8,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接PD,PE,则PD+PE的长度最小值为_____.
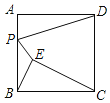
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com