
已知抛物线 y=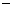 mx2+4x+2m与x轴交于点A(
mx2+4x+2m与x轴交于点A(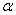 ,0)、B(
,0)、B(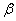 ,0),且
,0),且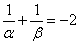 .
.
(1)求抛物线的解析式.
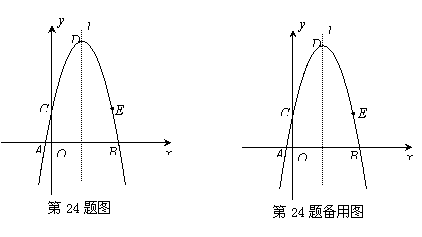
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l对称点为E.是否存在 x轴上的点M、y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形为平行四边形时,求点P的坐标.
 |
 (1)由题意可知,
(1)由题意可知,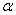 ,
,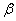 是方程
是方程 的两根,由根与系数的关系可得,
的两根,由根与系数的关系可得,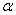 +
+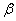 =
= ,
,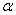
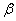 =-2.
=-2.
∵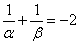 ,
,
∴ .即:
.即: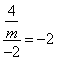 .
.
∴m=1.
∴抛物线解析式为 .
.
(2) 存在x轴,y轴上的点M,N,使得四边形DNME的周长最小.
∵ ,
,
∴抛物线的对称轴 为
为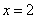 ,顶点D的坐标为(2,6).
,顶点D的坐标为(2,6).
又抛物线与y轴交点C的坐标为(0,2),点E与点C关于 对称,
对称,
∴E点坐标为(4,2).
作点D关于y轴的对称点D′,作点E关于x轴的对称点E′,
则D′坐标为(-2,6),E′坐标为(4,-2).连接D′E′,交x轴于M,交y轴与N.
此时,四边形DNME的周长最小为D′E′+DE.(如图1所示)
延长E′E, D′D交于一点F,在Rt△D′E′F中,D′F=6,E′F=8.
∴D′E′=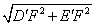 =
= .
.
 设对称轴
设对称轴 与CE交于点G,在Rt△DG E中,DG=4,EG=2.
与CE交于点G,在Rt△DG E中,DG=4,EG=2.
∴DE=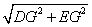 =
=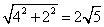 .
.
∴四边形DNME的周长的最小值为
10+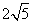 .
.
(3)如图2, P为抛物线上的点,过P作PH⊥x轴,垂足为H.若以点D、E、P、Q为顶点的四边形为平行四边形,则△PHQ≌△DGE.
∴PH=DG=4.
即 =4.
=4.
∴当y= 4时,
4时,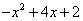 =4,解得
=4,解得
当y=-4时,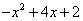 =-4,解得
=-4,解得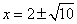 .
.
∴点P的坐标为( ,4),(
,4),( ,4),(
,4),( ,-4),(
,-4),( ,-4).
,-4).


科目:初中数学 来源: 题型:
射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为S甲2=0.51,S乙2=0.41、S丙2=0.62、S丁2=0.45,则四人中成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.
(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin53°=0.80,cos53°=0.60,tan53°=0.33,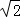 =1.41)
=1.41)

查看答案和解析>>
科目:初中数学 来源: 题型:
2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1、图2.
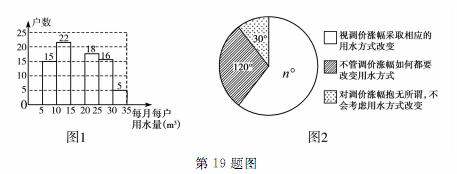
小明发现每月每户的用水量在5m3—35 m3之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
(1)n=_______,小明调查了_______户居民,并补全图1;
(2)每月每户用水量的中位数和众数分别落在什么范围?
(3)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-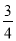 x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。

(1)求抛物线的解析式;
(2)若PE =5EF,求m的值;
(3)若点E/是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都区七校联谊九年级3月月考数学试卷(解析版) 题型:填空题
抛物线y=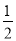 x2 向左平移8个单位,再向下平移9个单位后,所得抛物线的表达式是 .
x2 向左平移8个单位,再向下平移9个单位后,所得抛物线的表达式是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com