
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.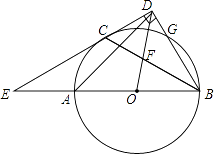
(1)求证:CD是⊙O的切线.
(2)若 ![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD= ![]() ,求AD的长.
,求AD的长.
【答案】
(1)证明:如图1,连接OC,AC,CG,
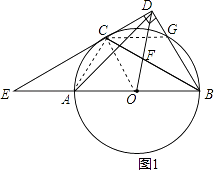
∵AC=CG,
∴ ![]() ,
,
∴∠ABC=∠CBG,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OCB=∠CBG,
∴OC∥BG,
∵CD⊥BG,
∴OC⊥CD,
∴CD是⊙O的切线
(2)解:∵OC∥BD,
∴△OCF∽△BDF,△EOC∽△EBD,
∴ ![]() ,
,
∴ ![]() ,
,
∵OA=OB,
∴AE=OA=OB,
∴OC= ![]() OE,
OE,
∵∠ECO=90°,
∴∠E=30°
(3)解:如图2,过A作AH⊥DE于H,
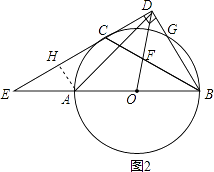
∵∠E=30°
∴∠EBD=60°,
∴∠CBD= ![]() EBD=30°,
EBD=30°,
∵CD= ![]() ,
,
∴BD=3,DE=3 ![]() ,BE=6,
,BE=6,
∴AE= ![]() BE=2,
BE=2,
∴AH=1,
∴EH= ![]() ,
,
∴DH=2 ![]() ,
,
在Rt△DAH中,AD= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)连接OC,AC,CG,由圆周角定理,得出∠ABC=∠CBG,再根据同圆的半径相等机等量代换求得∠OCB=∠CBG,根据平行线的判定得到OC∥BG,由已知CD⊥BG,得出OC⊥CD,即可证得结论。
(2)由OC∥BD,得出△OCF∽△BDF,△EOC∽△EBD,得出对应边成比例,再根据直角三角形的性质,可求出∠E的度数。
(3)过A作AH⊥DE于H,通过解直角三角形求出BD、BE、DE的长,在Rt△DAH中,根据勾股定理求出AD的长。


科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆检修车沿一段东西方向铁路检修,规定向东走为正,向西走为负,小组的出发地记为M,某天检修完毕时,行走记录(单位:千米)如下:
+12,-5,-9,+10,-4,+15,-9,+3,-6,-3,-7
(1)问收工时,检修小组距出发地M有多远?在东侧还是西侧?
(2)若检修车每千米耗油0.2升,求从出发到收工时检修车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):_______.
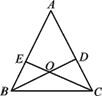
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( ) 
A.12
B.15
C.16
D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
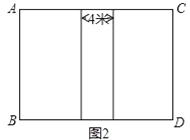
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com