
【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】给出下列判断:
①若|﹣a|=a,则a<0;
②有理数包括整数、0和分数;
③任何正数都大于它的倒数;
④2ax2﹣xy+y2是三次三项式;
⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负.
上述判断正确的有( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知△ABC,

(1)分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2;
(2)写出△A1B1C1和△A2B2C2各顶点坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;
信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.
根据以上信息,原来报名参加的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑电瓶车,乙骑自行车从相距17km的两地相向而行.
(1)甲、乙同时出发经过0.5h相遇,且甲每小时行程是乙每小时行程的3倍少6km.求乙骑自行车的速度.
(2)若甲、乙骑行速度保持与(1)中的速度相同,乙先出发0.5h,甲才出发,问甲出发几小时后两人相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.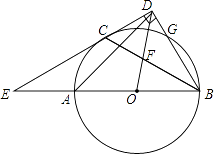
(1)求证:CD是⊙O的切线.
(2)若 ![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠CAB=30°,AC=8,半径为2的⊙O从点A开始(如图1)沿直线AB向右滚动,滚动时始终与直线AB相切(切点为D),当⊙O与△ABC只有一个公共点时滚动停止,作OG⊥AC于点G. 
(1)图1中,⊙O在AC边上截得的弦长AE=;
(2)当圆心落在AC上时,如图2,判断BC与⊙O的位置关系,并说明理由. 
(3)在⊙O滚动过程中,线段OG的长度随之变化,设AD=x,OG=y,求出y与x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
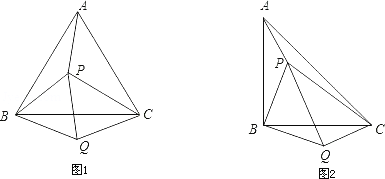
【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com