
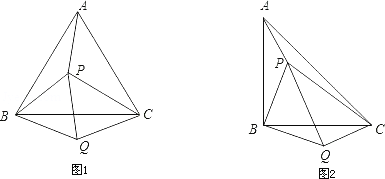
【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
【答案】(1)证明见解析(2)满足:![]()
【解析】
由旋转得△BAP≌△BCQ 满足:![]()
∴PA=CQ PB=BQ 由旋转得△BAP≌△BCQ
∵∠PBQ=60![]() ∴PA=CQ PB=BQ
∴PA=CQ PB=BQ
∴△PBQ为等边三角形 ∠PBQ=![]()
∴PB=PQ ∴![]()
∵PA![]() +PB
+PB![]() =PC
=PC![]() ∵
∵![]()
∴![]() ∴
∴![]()
∴∠PQC=90![]() ∴
∴![]()
(1)由旋转的性质可得到的条件是:①BP=BQ、PA=QC,②∠ABP=∠CBQ;
由②可证得∠PBQ=∠CBP+∠CBQ=∠CBP+∠ABP=∠ABC=60°,联立BP=BQ,即可得到△BPQ是等边三角形的结论,则BP=PQ;将等量线段代换后,即可得出PQ2+QC2=PC2,由此可证得∠PQC=90°;
(2)由(1)的解题思路知:△PBQ是等腰Rt△,则PQ2=2PB2,其余过程同(1),只不过所得结论稍有不同.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小阳骑车和步行的速度分别为270米/分钟和90米/分钟,小红每次从家步行到学校所需吋间相同,请根据两人的对话解决如下问题:
小阳:“如果我骑车,你步行,那么我从家到学校比你少用4分钟”;
小红:“如果我们俩都步行,那么从家到学校我比你少用2分钟.”若设小阳从家到学校的路程为![]() 米,小红从家到学校所需的时间为
米,小红从家到学校所需的时间为![]() 分钟:
分钟:
(1)小阳从家到学校骑车的时间是______分钟,步行的时间是_______分钟(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
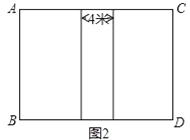
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来“低头族”现象日趋严重,初中生的视力状况受到了全社会的广泛关注.某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,并利用所得的数据绘制了如图的频数分布直方图,根据图中提供的信息解答下列问题: 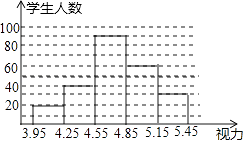
(1)本次调查共抽测了多少名学生?
(2)如果视力在4.9~5.1(含4.9和5.1)均属正常,那么全市约有多少名初中生的视力正常?
(3)若从视力在4.9~5.1的3个男生2个女生中随机抽取2人了解其平时用手机情况,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )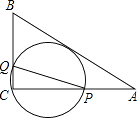
A.5
B.4 ![]()
C.4.75
D.4.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com