
如图,矩形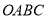 的顶点
的顶点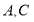 分别在
分别在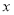 轴和
轴和 轴上,点
轴上,点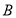 的坐标为
的坐标为 .双曲线
.双曲线 的图像经过
的图像经过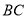 的中点
的中点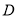 ,且与
,且与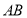 交于点
交于点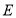 ,连接
,连接 .
.
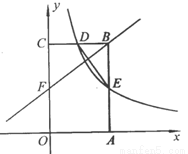
(1)求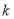 的值及点
的值及点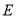 的坐标;
的坐标;
(2)若点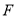 是边上一点,且ΔFCB∽ΔDBE,求直线
是边上一点,且ΔFCB∽ΔDBE,求直线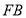 的解析式
的解析式
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:2014-2015学年重庆市巴南区九年级下学期期中质量监测数学试卷(解析版) 题型:填空题
从-1,1,2这三个数字中,随机抽取一个数,记为a,那么,使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为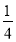 ,且使关于x的不等式组
,且使关于x的不等式组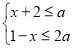 有解的概率为
有解的概率为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级学业水平模拟数学试卷(解析版) 题型:解答题
已知直线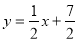 与茹
与茹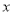 、
、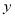 轴分别相交于B,A两点,抛物线
轴分别相交于B,A两点,抛物线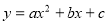 过A,B两点,且对称轴为直线
过A,B两点,且对称轴为直线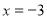 .
.
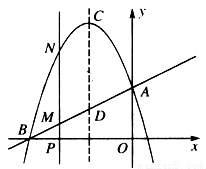
(1)求A,B两点的坐标,并求抛物线的解析式;
(2)若点P以1个单位/秒的速度从点B沿 轴向点O运动.过点P作
轴向点O运动.过点P作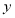 轴的平行线交直线AB于点M,交抛物线于点N.设点P运动的时间为
轴的平行线交直线AB于点M,交抛物线于点N.设点P运动的时间为 ,MN的长度为S,求S与
,MN的长度为S,求S与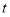 之间的函数关系式,并求出当
之间的函数关系式,并求出当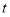 为何值时,S取得最大值?
为何值时,S取得最大值?
(3)设抛物线的对称轴CD与直线AB相交于点D,顶点为C.问:在(2)条件不变情况下,是否存在一个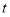 值,使四边形CDMN是平行四边形?若存在,求出
值,使四边形CDMN是平行四边形?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级学业水平模拟数学试卷(解析版) 题型:选择题
某校九年级四个班的代表队准备举行篮球友谊赛.甲、乙、丙三位同学预测比赛的 结果如下:
甲说:“902班得冠军,904班得第三”;
乙说:“901班得第四,903班得亚军”;
丙说:“903班得第三,904班得冠军”.
赛后得知,三人都只猜对了一半,则得冠军的是
A.901班 B.902班 C.903班 D.904班
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
如图,在正方形ABCD中, AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
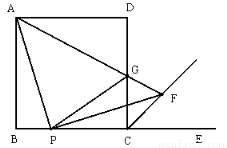
(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存在,求出BM的长度,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:选择题
如图,在等边△ABC中,点D、E分别是边AB、AC的中点.将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是
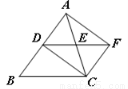
A.矩形 B.菱形 C.正方形 D.梯形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级中考第三次模拟数学试卷(解析版) 题型:解答题
问题提出:
平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
(1)当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);
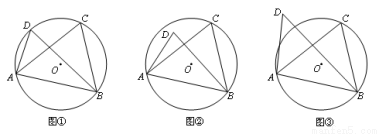
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.
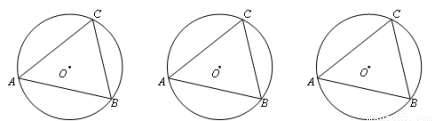
此时有 , 此时有 , 此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
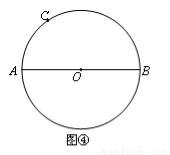
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA,CB;
②在上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com