
【题目】如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
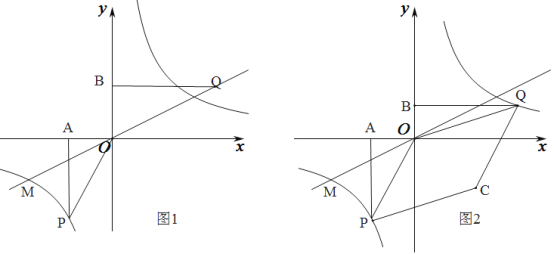
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;
(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.
【答案】(1)y=![]() x,
x,![]() ;(2)存在,Q1(2,1)和Q2(﹣2,﹣1);(3)2
;(2)存在,Q1(2,1)和Q2(﹣2,﹣1);(3)2![]() +4
+4
【解析】
(1)正比例函数和反比例函数的图象都经过点M(-2,-1),待定系数法可求它们解析式;
(2)由点Q在y=![]() x上,设出Q点坐标,表示△OBQ,由反比例函数图象性质,可知△OAP面积为1,则根据面积相等可构造方程,问题可解;
x上,设出Q点坐标,表示△OBQ,由反比例函数图象性质,可知△OAP面积为1,则根据面积相等可构造方程,问题可解;
(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,而点P(-1,-2)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.
解:(1)设正比例函数解析式为y=kx,
将点M(﹣2,﹣1)坐标代入得k=![]() ,所以正比例函数解析式为y=
,所以正比例函数解析式为y=![]() x,
x,
同样可得,反比例函数解析式为![]() ;
;
(2)当点Q在直线OM上运动时,
设点Q的坐标为Q(m,![]() m),
m),
于是S△OBQ=![]() OBBQ=
OBBQ=![]() ×
×![]() m×m=
m×m=![]() m2,
m2,
而S△OAP=|![]() (﹣1)×(﹣2)|=1,
(﹣1)×(﹣2)|=1,
所以有,![]() m2=1,解得m=±2,
m2=1,解得m=±2,
所以点Q的坐标为Q1(2,1)和Q2(﹣2,﹣1);
(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,
而点P(﹣1,﹣2)是定点,所以OP的长也是定长,
所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值,
因为点Q在第一象限中双曲线上,所以可设点Q的坐标为Q(n,![]() ),
),
由勾股定理可得OQ2=n2+![]() =(n﹣
=(n﹣![]() )2+4,
)2+4,
所以当(n﹣![]() )2=0即n
)2=0即n![]() =0时,OQ2有最小值4,
=0时,OQ2有最小值4,
又因为OQ为正值,所以OQ与OQ2同时取得最小值,
所以OQ有最小值2,由勾股定理得OP=![]() ,
,
所以平行四边形OPCQ周长的最小值是2(OP+OQ)=2(![]() +2)=2
+2)=2![]() +4.
+4.
(或因为反比例函数是关于y=x对称,所以当Q在反比例函数时候,OQ最短的时候,就是反比例与y=x的交点时候,联立方程组即可得到点Q坐标)


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 为圆心作⊙
为圆心作⊙![]() ,⊙
,⊙![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 为⊙
为⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,连接
的任意一点,连接![]() 、
、![]() ,过
,过![]() 点分别作
点分别作![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() .当
.当![]() 点在⊙
点在⊙![]() 上顺时针从点
上顺时针从点![]() 运动到点
运动到点![]() 的过程中,下列图象中能表示
的过程中,下列图象中能表示![]() 与
与![]() 的函数关系的部分图象是( )
的函数关系的部分图象是( )
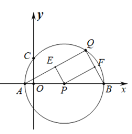
A.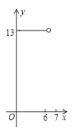 B.
B.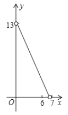 C.
C.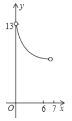 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 求一次函数
求一次函数![]() 的表达式;
的表达式;
![]() 若该商场获得利润为
若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
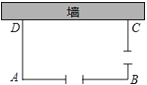
(1)若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为2cm的P的圆心在射线OA上,且与点O的距离为6cm,如果P以1cm/s的速度沿直线AB由A向B的方向移动,那么P与直线CD相切时☉P运动的时间是( )
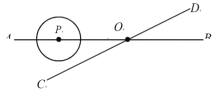
A.3秒或10秒B.3秒或8秒C.2秒或8秒D.2秒或10秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC:BC:AB=3:4:5,⊙O沿着△ABC的内部边缘滚动一圈,若⊙O的半径为1,且圆心O运动的路径长为18,则△ABC的周长为_____.
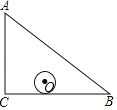
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com