
分析 (1)根据每个工人每天生产的产品个数以及每个产品的利润,表示出总利润即可;
(2)根据每天获取利润为14400元,则y=14400,求出即可;
(3)根据每天获取利润不低于15600元即y≥15600,求出即可.
解答 解:(1)根据题意得出:
y=12x×100+10(10-x)×180=-600x+18000;
(2)当y=14400时,有14400=-600x+18000,
解得:x=6.
故要派6名工人去生产甲种产品;
(3)根据题意可得,
y≥15600,
即-600x+18000≥15600,
解得:x≤4,
则10-x≥6.
故至少要派6名工人去生产乙种产品才合适.
点评 此题主要考查了一次函数的应用以及一元一次不等式的应用等知识,根据已知得出y与x之间的函数关系是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
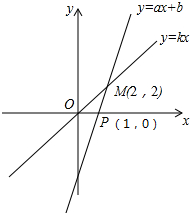 如图,一次函数y=ax+b的图象与正比例函数y=kx的图象交于点M.
如图,一次函数y=ax+b的图象与正比例函数y=kx的图象交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22015-1 | B. | 22015+1 | C. | $\frac{1}{2}$(22015-1) | D. | $\frac{1}{2}$(22015+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com