
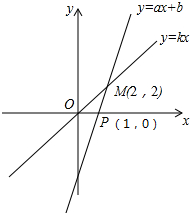
 如图,一次函数y=ax+b的图象与正比例函数y=kx的图象交于点M.
如图,一次函数y=ax+b的图象与正比例函数y=kx的图象交于点M.分析 (1)将(2,2)代入y=kx解出正比例函数的解析式,将(2,2)(1,0)代入一次函数解析式解答即可;
(2)根据图象得出不等式的解集即可;
(3)利用三角形的面积公式计算即可.
解答 解:(1)将(2,2)代入y=kx,解得:k=1,
所以正比例函数解析式为:y=x,
将(2,2)(1,0)代入一次函数解析式,可得:$\left\{\begin{array}{l}{2{k}_{1}+b=2}\\{{k}_{1}+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=2}\\{b=-2}\end{array}\right.$.
故一次函数的解析式为:y=2x-2;
(2)因为正比例函数的值大于一次函数的值,可得:x<2;
(3)△MOP的面积为:$\frac{1}{2}×1×2$=1.
点评 此题考查两条直线平行问题,关键是根据待定系数法解出解析式.


科目:初中数学 来源: 题型:选择题
| A. | 200cm2 | B. | 210cm2 | C. | 220cm2 | D. | 294cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
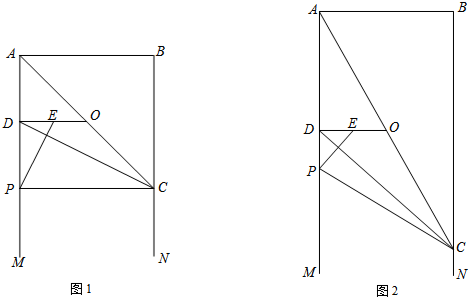
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
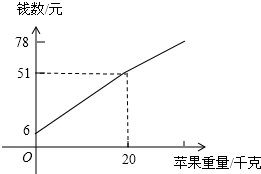 李大爷从家里的果园中摘了若干千克苹果.到城内出售,为了方便,他自带了一些零钱,将苹果按原来的市场价格出售一些后,由于急着回家,于是按原价的八折出售直到售完为止,售出苹果的千克数与他手中持有的钱数(含备用零钱)的关系如图所示,问:
李大爷从家里的果园中摘了若干千克苹果.到城内出售,为了方便,他自带了一些零钱,将苹果按原来的市场价格出售一些后,由于急着回家,于是按原价的八折出售直到售完为止,售出苹果的千克数与他手中持有的钱数(含备用零钱)的关系如图所示,问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 同时到达 | D. | 与路程有关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com