
| A. | 甲 | B. | 乙 | C. | 同时到达 | D. | 与路程有关 |
分析 甲乙二人相同的距离,时间、速度不同,因此可设总路程为1.乙到达目的地所用的时间为t1,甲到达目的地所用的时间为t2,由题意可得:t1=$\frac{\frac{1}{2}}{a}$+$\frac{\frac{1}{2}}{b}$=$\frac{a+b}{2ab}$;又$\frac{{t}_{2}}{2}$a+$\frac{{t}_{2}}{2}$b=1,所以t2=$\frac{2}{a+b}$,将t1、t2做差即可求出二者时间关系,即可求得答案.
解答 解:设总路程为单位1,乙到达目的地所用的时间为t1,甲到达目的地所用的时间为t2.
由题意可得:t1=$\frac{\frac{1}{2}}{a}$+$\frac{\frac{1}{2}}{b}$=$\frac{a+b}{2ab}$,
又∵$\frac{{t}_{2}}{2}$a+$\frac{{t}_{2}}{2}$b=1,
∴t2=$\frac{2}{a+b}$,
∴t1-t2=$\frac{a+b}{2ab}$-$\frac{2}{a+b}$=$\frac{(a+b)^{2}-4ab}{2ab(a+b)}$>0,
∴t1>t2,
(因为根据题意可得a≠b)所以乙先到.
故选:A.
点评 本题考查了列代数式,找到合适的等量关系是解决问题的关键.本题是一道考查行程问题的应用题,解此类问题只要把握住路程=速度×时间,即可找出等量关系,列出方程.要注意找出题中隐含的条件,如本题甲乙二人相同的行驶路程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
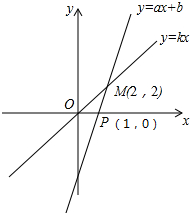 如图,一次函数y=ax+b的图象与正比例函数y=kx的图象交于点M.
如图,一次函数y=ax+b的图象与正比例函数y=kx的图象交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 |
| 2012年3月 | 3℃ | 5℃ | 3℃ | 5℃ | 6℃ | 8℃ |
| 2013年3月 | 6℃ | 6℃ | 11℃ | 14℃ | 15℃ | 14℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
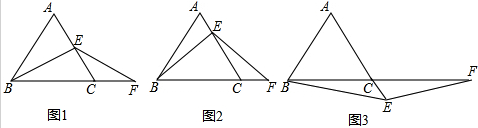
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com