
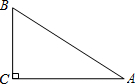
 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,分析 (1)由在Rt△ABC中,∠C=90°,∠A=30°,BC=1,利用三角函数,即可求得AC的长;
(2)由△ADB沿直线BD翻折后,将点A落在点E处,AD⊥ED,根据折叠的性质与垂直的定义,即可求得∠EDB与∠CDB的度数,继而可得△BCD是等腰直角三角形,求得CD的长,继而可求得答案.
解答 解:∵在Rt△ABC中,∠C=90°,∠A=30°,BC=1,
∴AC=$\frac{BC}{tan∠A}$=$\frac{1}{tan30°}$=$\sqrt{3}$,
∵将△ADB沿直线BD翻折后,将点A落在点E处,
∴∠ADB=∠EDB,DE=AD,
∵AD⊥ED,
∴∠CDE=∠ADE=90°,
∴∠EDB=∠ADB=$\frac{360°-90°}{2}$=135°,
∴∠CDB=∠EDB-∠CDE=135°-90°=45°,
∵∠C=90°,
∴∠CBD=∠CDB=45°,
∴CD=BC=1,
∴DE=AD=AC-CD=$\sqrt{3}$-1.
故答案为:$\sqrt{3}$;$\sqrt{3}$-1.
点评 此题考查了折叠的性质、直角三角形的性质以及等腰直角三角形性质.此题难度适中,注意数形结合思想的应用,注意折叠中的对应关系.


科目:初中数学 来源:2016-2017学年江苏省南通市七年级3月月考数学试卷(解析版) 题型:单选题
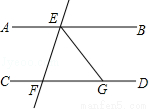
如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于( )
A. 36° B. 54° C. 72° D. 108°
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:填空题
在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,客车行驶时间为x(h),设客车离甲地的距离为y1(km),其中:y1=60x(0≤x≤10);出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象如图所示:
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,客车行驶时间为x(h),设客车离甲地的距离为y1(km),其中:y1=60x(0≤x≤10);出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
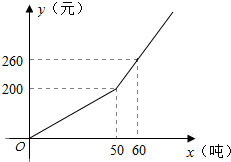 已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (-1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD顶点在y=$\frac{1}{x}$上,且S矩形ABCD=2$\sqrt{5}$,则A的坐标xA=$\frac{\sqrt{5}+1}{2}$,yA=$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD顶点在y=$\frac{1}{x}$上,且S矩形ABCD=2$\sqrt{5}$,则A的坐标xA=$\frac{\sqrt{5}+1}{2}$,yA=$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com