
 如图,矩形ABCD顶点在y=$\frac{1}{x}$上,且S矩形ABCD=2$\sqrt{5}$,则A的坐标xA=$\frac{\sqrt{5}+1}{2}$,yA=$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD顶点在y=$\frac{1}{x}$上,且S矩形ABCD=2$\sqrt{5}$,则A的坐标xA=$\frac{\sqrt{5}+1}{2}$,yA=$\frac{\sqrt{5}-1}{2}$. 分析 由题意可知A,B两点关于原点对称,从而得到点B的坐标,根据对角线互相平分的四边形是平行四边形可得S△APB=3,根据两点间的距离公式可得AB的长度,进而得到点P到直线AB的距离,设出点P的坐标,根据点到直线的距离公式即可求得点P的坐标.
解答 解:设A(x,$\frac{1}{x}$),
根据题意C(-x,-$\frac{1}{x}$),D($\frac{1}{x}$,x),
∵S矩形ABCD=2$\sqrt{5}$,
∴AD•CD=2$\sqrt{5}$,
∴${\sqrt{(x-\frac{1}{x})^{2}+(\frac{1}{x}-x)}}^{2}$•$\sqrt{(\frac{1}{x}+x)^{2}+(x+\frac{1}{x})^{2}}$=2$\sqrt{5}$,
∴$\sqrt{2}$(x-$\frac{1}{x}$)•$\sqrt{2}$(x+$\frac{1}{x}$)=2$\sqrt{5}$,
解得:x2=$\frac{\sqrt{5}+3}{2}$或x2=$\frac{\sqrt{5}-3}{2}$(不合题意舍去),
∴x1=$\frac{\sqrt{5}+1}{2}$,x2=$\frac{-\sqrt{5}-1}{2}$,
∴$\frac{1}{{x}_{1}}$=$\frac{\sqrt{5}-1}{2}$,$\frac{1}{{x}_{2}}$=$\frac{\sqrt{5}-1}{2}$,
∵点A在第一象限,
∴xA=$\frac{\sqrt{5}+1}{2}$,yA=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}+1}{2}$,$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题,反比例函数与正比例函数的交点关于原点对称;反比例函数的比例系数等于在它上面的点的横纵坐标的积,三角形面积公式以及点到直线的距离公式等知识点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
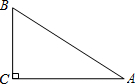 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的直径垂直于弦 | |
| B. | 正多边形是中心对称图形 | |
| C. | 四个角是直角的四边形是正方形 | |
| D. | 三角形的一条中线能将其分成面积相等的两部分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四边相等的四边形是菱形 | |
| B. | 一组对边相等,另一组对边平行的四边形是菱形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相平分的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
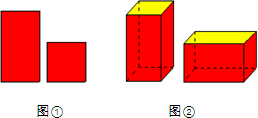 如图①的长方形和正方形纸板做侧面和底面,做成如图②的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果做这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可做70个.
如图①的长方形和正方形纸板做侧面和底面,做成如图②的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果做这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可做70个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条对角线相等的四边形是矩形 | |
| B. | 两条对角线互相平分的四边形是平行四边形 | |
| C. | 两条对角线互相垂直且相等的四边形是正方形 | |
| D. | 两条对角线互相垂直的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com