
【题目】如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据![]() )( )
)( )
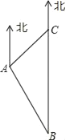
A. 7.3海里B. 10.3海里C. 17.3海里D. 27.3海里
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
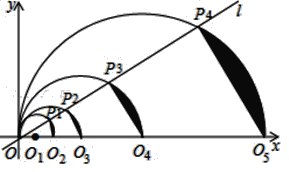
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=![]() x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和
x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和![]() 围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围
围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围![]() 成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和
成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和![]() 围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ABC=90°,BF为斜边上的高,在射线AB上有点D,连接DF,作∠DFE=90°,FE交射线BC于点E.
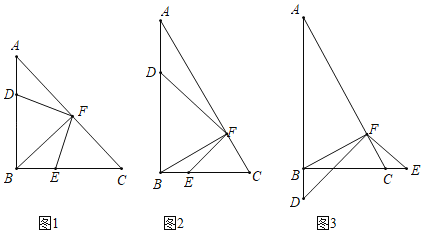
(问题发现)如图1所示,如果AB=CB,则DF与EF的数量关系为DF EF(选填>,<,=)
(类比探究)如图2所示,如果改变Rt△ABC中两直角边的比例,使得AB=2BC,则DF与EF还存在①中的关系吗?
(拓展延伸)如图3所示,在Rt△ABC中,如果已知BC=![]() ,AB=3,EF=
,AB=3,EF=![]() ,试求BD的长.
,试求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧AB的中点,弦CD与AB相交于E.
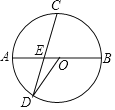
(1)若∠AOD=45°,求证:CE=![]() ED;(2)若AE=EO,求tan∠AOD的值.
ED;(2)若AE=EO,求tan∠AOD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
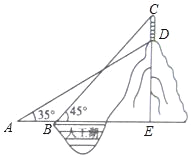
【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
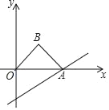
【题目】如图,直线y=![]() x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=
x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=![]() x﹣2上时,则△OAB平移的距离是_____.
x﹣2上时,则△OAB平移的距离是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
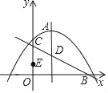
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标![]() ,顶点A的坐标为
,顶点A的坐标为![]() .直线
.直线![]() 交x轴于点B,交y轴于点C,与抛物线的对称轴交于点D,E为y轴上的一个动点.
交x轴于点B,交y轴于点C,与抛物线的对称轴交于点D,E为y轴上的一个动点.
(1)求这条抛物线的解析式和点D的坐标;
(2)若以C、D、E为顶点的三角形与△ACD相似,求点E的坐标;
(3)若点E关于直线BC的对称点M恰好落在抛物线上,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某景区门票价格为80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折(如打2折,即是按原价的20%出售),节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
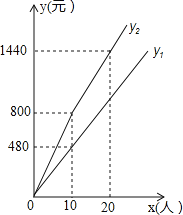
(1)a= ,b= ;
(2)直接写出y1、y2与x之间的函数关系式;
(3)一公司准备安排公司50名职工在“五一”假期时到此景区春游,而公司接到任务有一部分职工在“五一”当天需要加班,只能安排他们延期(非节假日)游玩,公司根据安排,春游期间除去其他费用,能提供的门票费用不超过3040元,那么公司至少安排多少人提前(五一期间)春游?
查看答案和解析>>
科目:初中数学 来源: 题型:
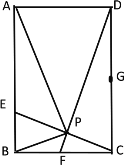
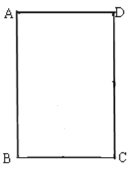
【题目】如图,矩形ABCD 中,AD=4cm,AB=6cm,动点 E从 B向A运动,速度为每秒2cm;同时,动点F从 C向B运动,速度为每秒3cm;任意一点到达终点后,两点都停止运动。连接CE、DF交于点P,连接BP,
(1)求证:△EBC ∽ △FCD
(2)BP最小值是多少?此时点F运动了多少秒?
(3)在该运动过程中, tan∠PAD的最大值是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com