
【题目】如图所示,在Rt△ABC中,∠ABC=90°,BF为斜边上的高,在射线AB上有点D,连接DF,作∠DFE=90°,FE交射线BC于点E.
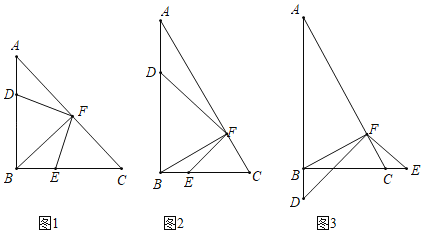
(问题发现)如图1所示,如果AB=CB,则DF与EF的数量关系为DF EF(选填>,<,=)
(类比探究)如图2所示,如果改变Rt△ABC中两直角边的比例,使得AB=2BC,则DF与EF还存在①中的关系吗?
(拓展延伸)如图3所示,在Rt△ABC中,如果已知BC=![]() ,AB=3,EF=
,AB=3,EF=![]() ,试求BD的长.
,试求BD的长.
【答案】【问题发现】:=;【类比探究】:不存在①中的关系,关系为:DF=2EF;【拓展延伸】:BD=![]() .
.
【解析】
问题发现:如图1,证明△ADF≌△BEF(SAS),得DF=EF;
类比探究:如图2所示,证明△ADF∽△BEF,得![]() ,则
,则![]() ,可得结论;
,可得结论;
拓展延伸:如图3,连接DE,设CE=a,根据勾股定理列等式:![]() ,解方程可得结论.
,解方程可得结论.
解:问题发现:
DF与EF的数量关系为DF=EF,理由是:
如图1,∵∠ABC=90°,AB=CB,
∴△ABC是等腰直角三角形,
∵BF⊥AC,
∴AF=CF=BF,∠ABF=∠CBF=45°,
∵∠AFD+∠BFD=∠BFD+∠BFE=90°,
∴∠AFD=∠BFE,
在△ADF和△BEF中,
∵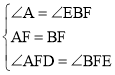 ,
,
∴△ADF≌△BEF(SAS),
∴DF=EF,
类比探究:
不存在①中的关系,关系为:DF=2EF,
理由是:如图2所示,∵∠A+∠ABF=∠A+∠C=90°,
∴∠ABF=∠C,
∵∠A=∠A,
∴△ABC∽△AFB,
∴![]() ,
,
∴![]() ,
,
∵∠A+∠ABF=∠ABF+∠CBF=90°,
∴∠A=∠CBF,
∵∠AFD+∠BFD=∠BFD+∠BFE=90°,
∴∠AFD=∠BFE,
在△ADF和△BEF中,
∵![]() ,
,
∴△ADF∽△BEF,
∴![]() ,
,
∵![]() ,AB=2BC,
,AB=2BC,
∴![]() ,
,
∴DF=2EF;
拓展延伸:
连接DE,设CE=a,
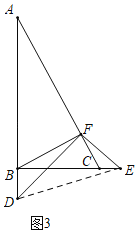
由以上结论可知: ![]() ,
,
∵EF=![]() ,CE=a,
,CE=a,
∴BD=![]() ,DF=
,DF=![]() ,
,
在Rt△DBE中,∠DBE=90°,得BD2+BE2=DE2,
在Rt△DFE中,∠DFE=90°,得DF2+EF2=DE2,
∴BD2+BE2=DF2+EF2,
即![]() ,
,
整理得:![]() ,
,
解得:a1=![]() ,a2=
,a2=![]() (舍),
(舍),
∴BD=![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上有点A、B,且点A表示﹣4,AB=10.
(1)点B表示的有理数为 .
(2)一只小虫从点A出发,以每秒1个单位长度的速度沿数轴正方向爬行到点C,点M、N分别是AC、BC的中点.
①若爬行4秒,则M表示数 ;N表示数 ;MN= .
②若爬行16秒,则M表示数 ;线段MN= .
③若爬行t秒,则线段MM= .
发现:点A、B、C在同一直线上,点M、N分别是AC、BC的中点,已知MN=a,则AB= (用含a的式子表示)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题
打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花费多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
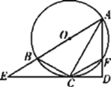
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,CE与⊙O切于点C,交AB的延长线于点E,过点A作AD⊥EC交EC的延长线于点D,交⊙O于点F,连接BC,CF.
(1)求证:AC平分∠BAD;
(2)若AD=6,∠BAF=60°,求四边形ABCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应上级教委的“海航招飞”号召,某校从九年级应届男生中抽取视力等生理指标合格的部分学生进行了文化课初检,教务处负责同志将测測试结果分为四个等级:甲、乙、丙、丁,然后将相关数据整理为两幅不完整的统计图,请依据相关信息解答下列问题:
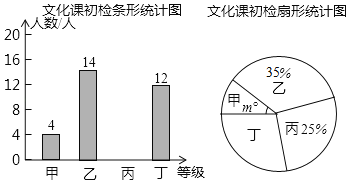
(1)本次参加文化课初检的男生人数为 ;
(2)扇形图中m的数值为 ,把条形统计图补充完整;
(3)据统计,全省生理指标过关的九年级男生有2400名左右,若规定文化课等级为“甲”“乙”的可进行文化课二检,请估计进入二检的男生有 ;
(4)本次抽检进入“甲”等的4名男生中九(1)、九(2)班各占2名,若从“甲”等学生中随机抽取两名男生进行调研,请用树形图表示抽到的两名男生恰为九(1)班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题做如下探究:
(问题背景)
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.小明同学探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图②),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
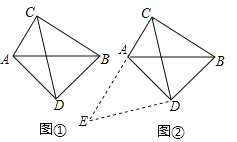
(简单应用)
(1)在图①中,若AC=![]() ,BC=2
,BC=2![]() ,则CD= .
,则CD= .
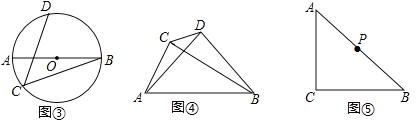
(2)如图③,AB是⊙O的直径,点C、D在⊙O上,![]() ,若AB=10,BC=8,求CD的长.
,若AB=10,BC=8,求CD的长.
(拓展延伸)
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=a,BC=b(a<b),求CD的长.(用含a,b的代数式表示).
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,请直接写出线段PQ与AC的数量关系.
AC,CE=CA,点Q为AE的中点,请直接写出线段PQ与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据![]() )( )
)( )
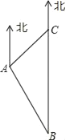
A. 7.3海里B. 10.3海里C. 17.3海里D. 27.3海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
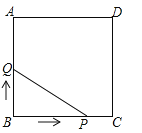
A.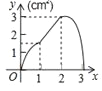 B.
B.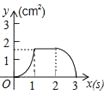 C.
C.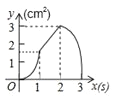 D.
D.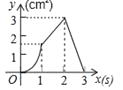
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com