
【题目】小明在一次数学兴趣小组活动中,对一个数学问题做如下探究:
(问题背景)
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.小明同学探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图②),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
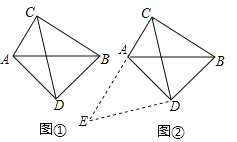
(简单应用)
(1)在图①中,若AC=![]() ,BC=2
,BC=2![]() ,则CD= .
,则CD= .
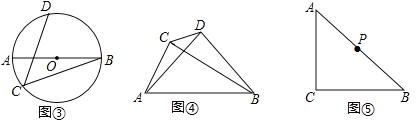
(2)如图③,AB是⊙O的直径,点C、D在⊙O上,![]() ,若AB=10,BC=8,求CD的长.
,若AB=10,BC=8,求CD的长.
(拓展延伸)
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=a,BC=b(a<b),求CD的长.(用含a,b的代数式表示).
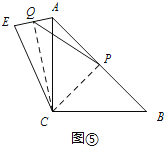
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,请直接写出线段PQ与AC的数量关系.
AC,CE=CA,点Q为AE的中点,请直接写出线段PQ与AC的数量关系.
【答案】(1)![]() ;(2)7
;(2)7![]() ;(3)CD=
;(3)CD=![]() ;(4)线段PQ与AC的数量关系是
;(4)线段PQ与AC的数量关系是![]() 或
或![]() .
.
【解析】
(1)由题意可知:AC+BC=![]() CD,所以将AC与BC的长度代入即可得出CD的长度;
CD,所以将AC与BC的长度代入即可得出CD的长度;
(2)连接AC、BD、AD即可将问题转化为第(1)问的问题,利用题目所给出的证明思路即可求出CD的长度;
(3)以AB为直径作⊙O,连接OD并延长交⊙O于点D1,由(2)问题可知:AC+BC=![]() CD1;又因为CD1=D1D,所以利用勾股定理即可求出CD的长度;
CD1;又因为CD1=D1D,所以利用勾股定理即可求出CD的长度;
(4)根据题意可知:点E的位置有两种,分别是当点E在直线AC的右侧和当点E在直线AC的左侧时,连接CQ、CP后,利用(2)和(3)问的结论进行解答.
(1)由题意可得:AC+BC=![]() CD,
CD,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
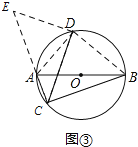
(2)连接AC、BD、AD,
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵AD=BD,
将△BCD绕点D顺时针旋转90°到△AED处,如图③,
∴∠EAD=∠DBC,
∵∠DBC+∠DAC=180°,
∴∠EAD+∠DAC=180°,
∴E、A、C三点共线,
∵AB=10,BC=8,
∴由勾股定理可求得:AC=6,
∵BC=AE,
∴CE=AE+AC=14,
∵∠EDA=∠CDB,
∴∠EDA+∠ADC=∠CDB+∠ADC,
即∠EDC=∠ADB=90°,
∵CD=ED,
∴△EDC是等腰直角三角形,
∴CE=![]() CD,
CD,
∴CD=7![]() ;
;
(3)以AB为直径作⊙O,连接OD并延长交⊙O于点D1,
连接D1A,D1B,D1C,如图④
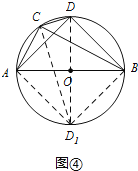
由(2)的证明过程可知:AC+BC=![]() D1C,
D1C,
∴![]() ,
,
又∵D1D是⊙O的直径,
∴∠DCD1=90°,
∵AC=a,BC=b,
∴由勾股定理可求得:AB2=a2+b2,
∴D1D2=AB2=a2+b2,
∵D1C2+CD2=D1D2,
∴CD2=a2+b2﹣![]() ,
,
∵a<b,
∴![]() ;
;
(4)当点E在直线AC的左侧时,如图⑤,
连接CQ,PC,
∵AC=BC,∠ACB=90°,
点P是AB的中点,
∴AP=CP,∠APC=90°,
又∵CA=CE,点Q是AE的中点,
∴∠CQA=90°,
设AC=a,
∵AE=![]() ,
,
∴![]() ,
,
∴![]() ,
,
由勾股定理可求得:![]() ,
,
由(2)的证明过程可知:AQ+CQ=![]() PQ,
PQ,
∴![]() ,
,
∴![]() ,
,
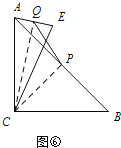
当点E在直线AC的右侧时,如图⑥,
连接CQ、CP,
同理可知:∠AQC=∠APC=90°,
设AC=a,
∴![]() ,
,
由勾股定理可求得:![]() ,
,
由(3)的结论可知:![]() ,
,
∴![]() ,
,
综上所述,线段PQ与AC的数量关系是![]() 或
或![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,![]() 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论![]() ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:
小青:![]() ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;
小夏:![]() ;小雨:
;小雨:![]() .
.
这四位同学写出的结论中不正确的是![]()
![]()

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ABC=90°,BF为斜边上的高,在射线AB上有点D,连接DF,作∠DFE=90°,FE交射线BC于点E.
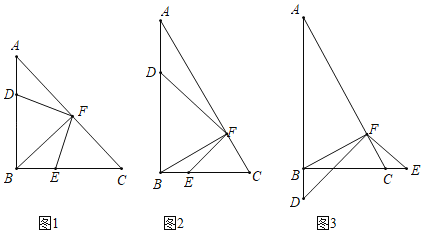
(问题发现)如图1所示,如果AB=CB,则DF与EF的数量关系为DF EF(选填>,<,=)
(类比探究)如图2所示,如果改变Rt△ABC中两直角边的比例,使得AB=2BC,则DF与EF还存在①中的关系吗?
(拓展延伸)如图3所示,在Rt△ABC中,如果已知BC=![]() ,AB=3,EF=
,AB=3,EF=![]() ,试求BD的长.
,试求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧AB的中点,弦CD与AB相交于E.
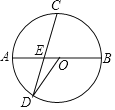
(1)若∠AOD=45°,求证:CE=![]() ED;(2)若AE=EO,求tan∠AOD的值.
ED;(2)若AE=EO,求tan∠AOD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
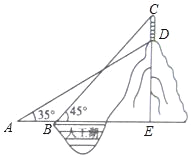
【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
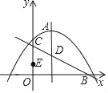
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标![]() ,顶点A的坐标为
,顶点A的坐标为![]() .直线
.直线![]() 交x轴于点B,交y轴于点C,与抛物线的对称轴交于点D,E为y轴上的一个动点.
交x轴于点B,交y轴于点C,与抛物线的对称轴交于点D,E为y轴上的一个动点.
(1)求这条抛物线的解析式和点D的坐标;
(2)若以C、D、E为顶点的三角形与△ACD相似,求点E的坐标;
(3)若点E关于直线BC的对称点M恰好落在抛物线上,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:
月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:![]() 书法比赛;
书法比赛;![]() 国画竞技;
国画竞技;![]() 诗歌朗诵;
诗歌朗诵;![]() 汉字大赛;
汉字大赛;![]() 古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
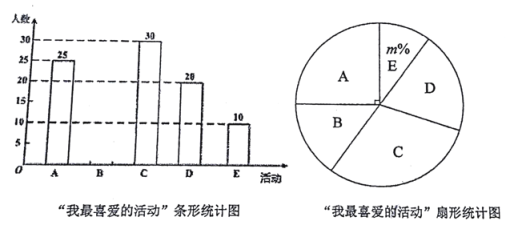
(1)此次催记抽取的初三学生共 人,![]() ,并补全条形统计图;
,并补全条形统计图;
(2)初三年级准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用树状图或列表法求选出的两名选手正好是一男一女的概率是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com