
【题目】已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.

【答案】(1)证明见解析(2)![]() (3)没有变化,理由见解析
(3)没有变化,理由见解析
【解析】(1)证明:∵四边形ABCD是正方形,∴∠ABE=∠BCF=90°,AB=BC。∴∠ABF+∠CBF=90°。
∵AE⊥BF,∴∠ABF+∠BAE=90°。∴∠BAE=∠CBF。
在△ABE和△BCF中,∵∠ABE=∠BCF,AB=BC,∠BAE=∠CBF,
∴△ABE≌△BCF(ASA)。
(2)解:∵正方形面积为3,∴AB=![]() 。
。
在△BGE与△ABE中,∵∠GBE=∠BAE,∠EGB=∠EBA=90°,∴△BGE∽△ABE。
∴![]() 。
。
又∵BE=1,∴AE2=AB2+BE2=3+1=4。
∴![]() 。
。
(3)解:没有变化。理由如下:
∵AB=![]() ,BE=1,∴
,BE=1,∴![]() 。∴∠BAE=30°。
。∴∠BAE=30°。
∵AB′=AD,∠AB′E′=∠ADE'=90°,AE′= AE′,∴Rt△ABE≌Rt△AB′E′≌Rt△ADE′,
∴∠DAE′=∠B′AE′=∠BAE=30°。
∴AB′与AE在同一直线上,即BF与AB′的交点是G。
设BF与AE′的交点为H,
则∠BAG=∠HAG=30°,而∠AGB=∠AGH=90°,AG= AG,∴△BAG≌△HAG。
∴![]() 。
。
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化。
(1)由四边形ABCD是正方形,可得∠ABE=∠BCF=90°,AB=BC,又由AE⊥BF,由同角的余角相等,即可证得∠BAE=∠CBF,然后利用ASA,即可判定:△ABE≌△BCF。
(2)由正方形ABCD的面积等于3,即可求得此正方形的边长,由在△BGE与△ABE中,∠GBE=∠BAE,∠EGB=∠EBA=90°,可证得△BGE∽△ABE,由相似三角形的面积比等于相似比的平方,即可求得答案。
(3)由正切函数,求得∠BAE=30°,易证得Rt△ABE≌Rt△AB′E′≌Rt△ADE′,可得AB′与AE在同一直线上,即BF与AB′的交点是G,然后设BF与AE′的交点为H,可证得△BAG≌△HAG,从而证得结论


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: ① abc<0;② 2a+b=0; ③ b2-4ac<0;④ 9a+3b+c>0; ⑤ c+8a<0.正确的结论有( ).
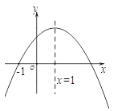
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有点A、B,且点A表示﹣4,AB=10.
(1)点B表示的有理数为 .
(2)一只小虫从点A出发,以每秒1个单位长度的速度沿数轴正方向爬行到点C,点M、N分别是AC、BC的中点.
①若爬行4秒,则M表示数 ;N表示数 ;MN= .
②若爬行16秒,则M表示数 ;线段MN= .
③若爬行t秒,则线段MM= .
发现:点A、B、C在同一直线上,点M、N分别是AC、BC的中点,已知MN=a,则AB= (用含a的式子表示)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2019的坐标为( )
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2019的坐标为( )
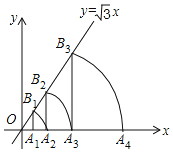
A. (22017,0)B. (22018,0)C. (22020,0)D. (24034,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可销售20件每件盈利40元.为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件,求:
(1)若商场每件衬衫降价10元,则商场每天可盈利多少元?
(2)若商场平均每天要盈利1250元,每件衬衫应降价多少元?
(3)要使商场平均每天盈利1500元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组就“最想去的漳州5个最美乡村”随机调查了本校部分学生. 要求每位同学选择且只能选择一个最想去的最美乡村. 下面是根据调查结果绘制出的尚不完整统计表和统计图,其中x、y是满足x<y的正整数.
最美乡村意向统计表
最美乡村 | 人数 |
A:龙海埭美村 | 10 |
B:华安官畬村 | 11 |
C:长泰山重村 | 4x |
D:南靖塔下村 | 9 |
E:东山澳角村 | 3y |
最美乡村意向扇形统计图
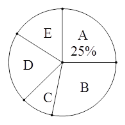
根据以上信息,解答下列问题:
(1)求x、y的值;
(2)若该校有1200名学生,请估计“最想去华安官畬村”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题
打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花费多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题做如下探究:
(问题背景)
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.小明同学探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图②),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
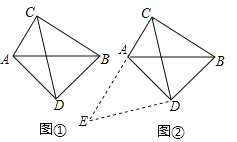
(简单应用)
(1)在图①中,若AC=![]() ,BC=2
,BC=2![]() ,则CD= .
,则CD= .
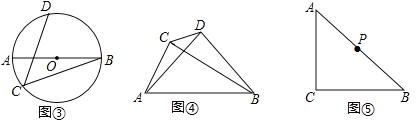
(2)如图③,AB是⊙O的直径,点C、D在⊙O上,![]() ,若AB=10,BC=8,求CD的长.
,若AB=10,BC=8,求CD的长.
(拓展延伸)
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=a,BC=b(a<b),求CD的长.(用含a,b的代数式表示).
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,请直接写出线段PQ与AC的数量关系.
AC,CE=CA,点Q为AE的中点,请直接写出线段PQ与AC的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com