
【题目】某商场销售一批名牌衬衫,平均每天可销售20件每件盈利40元.为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件,求:
(1)若商场每件衬衫降价10元,则商场每天可盈利多少元?
(2)若商场平均每天要盈利1250元,每件衬衫应降价多少元?
(3)要使商场平均每天盈利1500元,可能吗?请说明理由.
【答案】(1)商场每天可盈利1200元;(2)每件衬衫应降价15元;(3)不可能,理由见解析.
【解析】
(1)根据降价10元求出每天盈利的钱即可;
(2)设每件衬衫降价x元,根据题意列出方程,求出方程的解即可得到结果;
(3)设每件衬衫降价y元,根据题意列出方程,求出方程的解即可得到结果.
(1)降价10元,每天可多售出10件,
(40﹣10)×(20+20)=1200,
答:商场每天可盈利1200元;
(2)设每件衬衫降价x元,
依题意得:(40﹣x)(20+10×![]() )=1250,
)=1250,
化简得:x2﹣30x+225=0,
解得:x1=x2=15,
答:每件衬衫应降价15元;
(3)不可能,理由是:
假设每件衬衫降价y元时,商场平均每天盈利1500元,
(40﹣y)(20+10×![]() )=1500,
)=1500,
化简得:y2﹣30y+350=0,
∵△=900﹣1400=﹣500<0,
∴原方程无实数根,
则不可能.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品中,大笔记本购买的数量是____本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸飞机是我们儿时快乐的回忆,现有一张长为290mm,宽为200mm的白纸,如图所示,以下面几个步骤折出纸飞机:(说明:第一步:白纸沿着EF折叠,AB边的对应边A′B′与边CD平行,将它们的距离记为x;第二步:将EM,MF分别沿着MH,MG折叠,使EM与MF重合,从而获得边HG与A′B′的距离也为x),则PD=______mm.
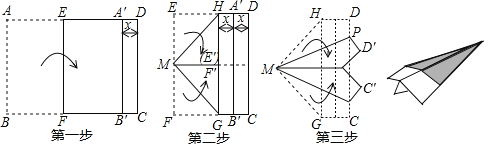
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC、BD相交于点O,点E是BC的中点,AE交BD于点F,BH⊥AE于点G,连接OG,则下列结论中①OF=OH,②△AOF∽△BGF,③tan∠GOH=2,④FG+CH=![]() GO,正确的个数是( )
GO,正确的个数是( )
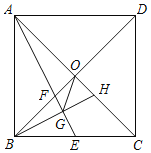
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=![]() x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和
x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和![]() 围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围
围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围![]() 成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和
成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和![]() 围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
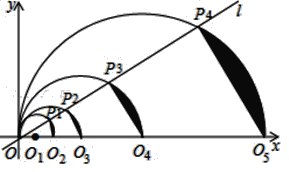
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进郴州市创建国家森林城市工作,尽快实现“让森林走进城市,让城市拥抱森林”的构想,今年三月份,某县园林办购买了甲、乙两种树苗共1000棵,其中甲种树苗每棵40元,乙种树苗每棵50元,据相关资料表明:甲、乙两种树苗的成活率分别为85%和90%.
(1)若购买甲、乙两种树苗共用去了46500元,则购买甲、乙两种树苗各多少棵?
(2)若要使这批树苗的成活率不低于88%,则至多可购买甲种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧AB的中点,弦CD与AB相交于E.
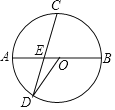
(1)若∠AOD=45°,求证:CE=![]() ED;(2)若AE=EO,求tan∠AOD的值.
ED;(2)若AE=EO,求tan∠AOD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com