
����Ŀ��Ϊ�ƽ������д�������ɭ�ֳ��й���������ʵ������ɭ���߽����У��ó���ӵ��ɭ�����Ĺ��룬�������·ݣ�ij���ְ칺���˼ס����������繲1000�ã����м�������ÿ��40Ԫ����������ÿ��50Ԫ����������ϱ������ס�����������ijɻ��ʷֱ�Ϊ85%��90%��
��1��������ס����������繲��ȥ��46500Ԫ������ס���������������ٿã�
��2����Ҫʹ��������ijɻ��ʲ�����88%��������ɹ������������ٿã�
���𰸡���1��350��650����2��400.
��������
���⣨1�����̵�Ӧ�ý���ؼ������δ֪�����ҳ��ص�����ϵ���г��������.�����蹺��ס������������x�ú�y�ã����ݼס����������繲1000�źͼס����������繲��ȥ��46500Ԫ���г������飬������⼴��.
��2������ʽ��Ӧ�ý���ؼ����ҳ���������ϵ���г�����ʽ���.����������ɹ����������x�ã�������������Ϊ��1000��x���ã�������������ijɻ��ʲ�����88%���г�����ʽ����⼴�ɣ�
�����������1���蹺��ס������������x�ú�y�ã���������ã�
![]() ��
��
��ã�![]() ��
��
�𣺹���ס������������350�ú�650��.
��2��������ɹ����������x�ã�������������Ϊ��1000��x���ã���������ã�
![]() ��
��
���x��400��
������ɹ����������400�ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
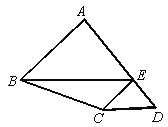
����Ŀ����ͼ�����ı���ABCD �У���E��AD�ϣ�EC��AB��EB��DC������ABE���Ϊ5����ECD�����Ϊ1������BCE�������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ�������20��ÿ��ӯ��40Ԫ��Ϊ���������ۣ�����ӯ�����������ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ������ÿ����5Ԫ���̳�ƽ��ÿ��ɶ��۳�10������
��1�����̳�ÿ����������10Ԫ�����̳�ÿ���ӯ������Ԫ��
��2�����̳�ƽ��ÿ��Ҫӯ��1250Ԫ��ÿ������Ӧ���۶���Ԫ��
��3��Ҫʹ�̳�ƽ��ÿ��ӯ��1500Ԫ����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
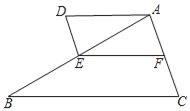
����Ŀ����ͼ����֪��D����ABC���ⲿ��AD��BC����E�ڱ�AB�ϣ�ABAD��BCAE��
��1����֤����BAC����AED��
��2���ڱ�ACȡһ��F�������AFE����D����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з���(��)��Ӧ����
����ǰ����60��A��Ʒ��30��B��Ʒ����1080Ԫ����50��A��Ʒ��10��B��Ʒ����840Ԫ�����ۺ���500��A��Ʒ��500��B��Ʒ����9600Ԫ���Ȳ������ٻ��Ѷ���Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+![]() x+c��x�ύ��A��B���㣬��y�ύ��C�㣬��A(2��0)��C(0��-4)��ֱ��l��y=-
x+c��x�ύ��A��B���㣬��y�ύ��C�㣬��A(2��0)��C(0��-4)��ֱ��l��y=-![]() x-4��x�ύ�ڵ�D����P��������y=ax2+
x-4��x�ύ�ڵ�D����P��������y=ax2+![]() x+c�ϵ�һ���㣬����P��PE��x�ᣬ����ΪE����ֱ��l��F��
x+c�ϵ�һ���㣬����P��PE��x�ᣬ����ΪE����ֱ��l��F��
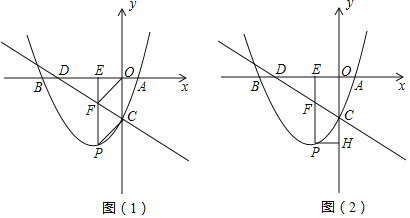
(1)����������߱���ʽ��
(2)��ͼ(1)������P�ڵ������ޣ��ı���PCOF��ƽ���ı��Σ���P������ꣻ
(3)��ͼ(2)������AC����֤����ACD��ֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
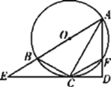
����Ŀ����ͼ����֪ABΪ��O��ֱ����CΪ��O��һ�㣬CE���O���ڵ�C����AB���ӳ����ڵ�E������A��AD��EC��EC���ӳ����ڵ�D������O�ڵ�F������BC��CF��
(1)��֤��ACƽ�֡�BAD��
(2)��AD��6����BAF��60�������ı���ABCF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ⲻ��ʽ�� ���������С�����������������ĺͣ�
���������С�����������������ĺͣ�
��2���Ȼ�������ֵ![]() ������x���㷽��x2+x��2��0��
������x���㷽��x2+x��2��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣮Ϊ�˴����л��������㴫ͳ�Ļ�������ij��ѧ���С�������д��������������������ѧ���ijɼ�����ѧ���ijɼ���ΪA��B��C��D�ĸ��ȼ�������������Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������������

�������ͳ��ͼ����������⣺
��1���μӱ�����ѧ������____����
��2��������ͳ��ͼ�У�m��ֵΪ____����ʾ��D�ȼ��������ε�Բ�Ľ�Ϊ____�ȣ�
��3����ί������ӱ��α������A�ȼ���ѧ���У�ѡ��2��ȥ�μ�ȫ����ѧ����������д����������֪A�ȼ�ѧ����������1���������б�������״ͼ�������ѡ2��ѧ��ǡ����һ��������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com