
【题目】如图,已知抛物线y=ax2+![]() x+c与x轴交于A,B两点,与y轴交于C点,且A(2,0),C(0,-4),直线l:y=-
x+c与x轴交于A,B两点,与y轴交于C点,且A(2,0),C(0,-4),直线l:y=-![]() x-4与x轴交于点D,点P是抛物线y=ax2+
x-4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于F.
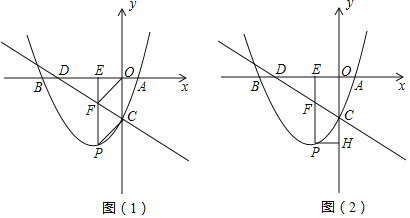
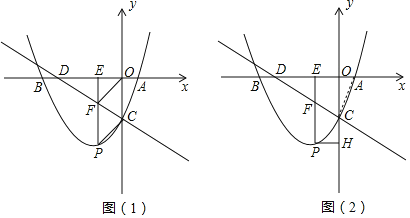
(1)试求该抛物线表达式;
(2)如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;
(3)如图(2),连接AC.求证:△ACD是直角三角形.
【答案】(1)y=![]() x2+
x2+![]() x-4;(2)P点的坐标为(-8,-4),(-2.5,-
x-4;(2)P点的坐标为(-8,-4),(-2.5,-![]() );(3)证明见解析.
);(3)证明见解析.
【解析】
(1)利用待定系数法即可求a、c的值,从而求得抛物线的表达式;
(2)设P点的坐标是(x,![]() x2+
x2+![]() x-4),则F(x,-
x-4),则F(x,-![]() x-4),由OCPF是平行四边形得OC=FP,OC∥PF,从而-
x-4),由OCPF是平行四边形得OC=FP,OC∥PF,从而-![]() x2-
x2-![]() x=4,求解即可得P的横坐标,代入解析式即可得P的坐标.
x=4,求解即可得P的横坐标,代入解析式即可得P的坐标.
(3)分别求出点A、C、D的坐标,可以根据勾股定理的逆定理即可判断
(1)依题意,抛物线经过A(2,0),C(0,-4),则c=-4
将点A代入得0=4a+![]() ×2-4,解得a=
×2-4,解得a=![]()
抛物线的解析式是y=![]() x2+
x2+![]() x-4
x-4
(2)设P点的坐标是(x,![]() x2+
x2+![]() x-4),则F(x,-
x-4),则F(x,-![]() x-4)
x-4)
∴PF=(-![]() x-4)-(
x-4)-(![]() x2+
x2+![]() x-4)=-
x-4)=-![]() x2-
x2-![]() x
x
∵四边形OCPF是平行四边形
∴OC=FP,OC∥PF
∴-![]() x2-
x2-![]() x=4
x=4
即2x2+21x+40=0
解得x1=-8x2=-2.5
∴P点的坐标为(-8,-4),(-2.5,-![]() )
)
(3)当y=0时,-![]() x-4=0,得x=-8,即D(-8,0)
x-4=0,得x=-8,即D(-8,0)
当x=0时,0-4=y,即C(0,-4)
当y=0时,![]() x2+
x2+![]() x-4=0
x-4=0
解得x1=-10x2=2,即B(-10,0),A(2,0)
∴AD=10
∵AC2=22+42=20
CD2=82+42=80
∴AD2=AC2+CD2
∴∠ACD=90°△ACD是直角三角形


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
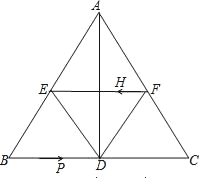
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC、BD相交于点O,点E是BC的中点,AE交BD于点F,BH⊥AE于点G,连接OG,则下列结论中①OF=OH,②△AOF∽△BGF,③tan∠GOH=2,④FG+CH=![]() GO,正确的个数是( )
GO,正确的个数是( )
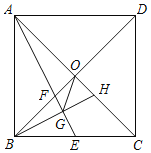
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“学习朱子文化,弘扬理学思想”为主题的读书月活动,并向学生征集读后感,学校将收到的读后感篇数按年级进行统计,绘制了以下两幅统计图(不完整).
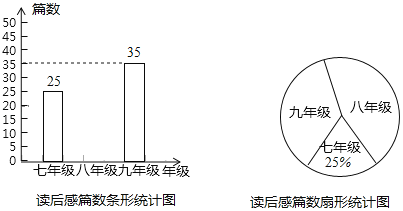
据图中提供的信息完成以下问题
(1)扇形统计图中“八年级”对应的圆心角是 °,并补全条形统计图;
(2)经过评审,全校有4篇读后感荣获特等奖,其中有一篇来自七年级,学校准备从特等奖读后感中任选两篇在校广播电台上播出,请利用画树状图或列表的方法求出七年级特等奖读后感被校广播电台播出的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进郴州市创建国家森林城市工作,尽快实现“让森林走进城市,让城市拥抱森林”的构想,今年三月份,某县园林办购买了甲、乙两种树苗共1000棵,其中甲种树苗每棵40元,乙种树苗每棵50元,据相关资料表明:甲、乙两种树苗的成活率分别为85%和90%.
(1)若购买甲、乙两种树苗共用去了46500元,则购买甲、乙两种树苗各多少棵?
(2)若要使这批树苗的成活率不低于88%,则至多可购买甲种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
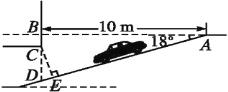
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC与△DEF均为等边三角形,且AB=2,DB=1,现△ABC静止不动,△DEF沿着直线EC以每秒1个单位的速度向右移动设△DEF移动的时间为x,△DEF与△ABC重合的面积为y,则能大致反映y与x函数关系的图象是( )
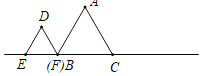
A.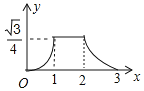 B.
B.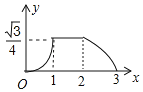
C.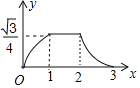 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=4,b=5,则该矩形的面积为( )
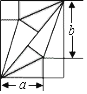
A.50B.40C.30D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com