
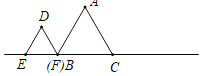
【题目】如图所示,已知△ABC与△DEF均为等边三角形,且AB=2,DB=1,现△ABC静止不动,△DEF沿着直线EC以每秒1个单位的速度向右移动设△DEF移动的时间为x,△DEF与△ABC重合的面积为y,则能大致反映y与x函数关系的图象是( )
A.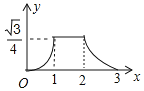 B.
B.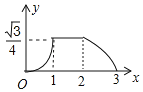
C.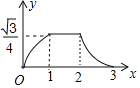 D.
D.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
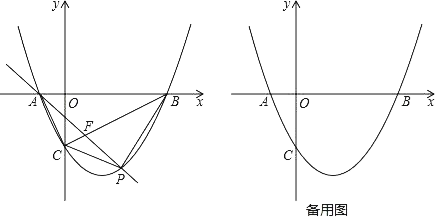
(1)求A,B两点的坐标.
(2)点P是线段BC下方的抛物线上的动点,连结PC,PB.
①是否存在一点P,使△PBC的面积最大,若存在,请求出△PBC的最大面积;若不存在,试说明理由.
②连结AC,AP,AP交BC于点F,当∠CAP=∠ABC时,求直线AP的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在△ABC的外部,AD∥BC,点E在边AB上,ABAD=BCAE.
(1)求证:∠BAC=∠AED;
(2)在边AC取一点F,如果∠AFE=∠D,求证:![]() .
.
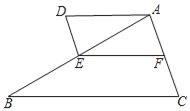
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+![]() x+c与x轴交于A,B两点,与y轴交于C点,且A(2,0),C(0,-4),直线l:y=-
x+c与x轴交于A,B两点,与y轴交于C点,且A(2,0),C(0,-4),直线l:y=-![]() x-4与x轴交于点D,点P是抛物线y=ax2+
x-4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于F.
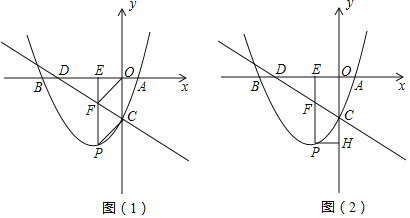
(1)试求该抛物线表达式;
(2)如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;
(3)如图(2),连接AC.求证:△ACD是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,CE与⊙O切于点C,交AB的延长线于点E,过点A作AD⊥EC交EC的延长线于点D,交⊙O于点F,连接BC,CF.
(1)求证:AC平分∠BAD;
(2)若AD=6,∠BAF=60°,求四边形ABCF的面积.
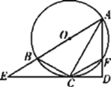
查看答案和解析>>
科目:初中数学 来源: 题型:
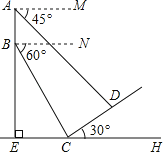
【题目】夏季多雨,在山坡CD处出现了滑坡,为了测量山体滑坡的坡面长度CD,探测队在距离坡底C点![]() 米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
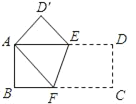
【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A、C重合,若其长BC为8,宽AB为4.
(1)求证:△AEF是等腰三角形.
(2)EF= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com