
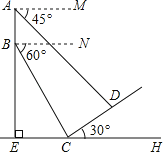
【题目】夏季多雨,在山坡CD处出现了滑坡,为了测量山体滑坡的坡面长度CD,探测队在距离坡底C点![]() 米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
【答案】山体滑坡的坡面长度CD的长为(570![]() ﹣810)米.
﹣810)米.
【解析】
作DG⊥AE于G,DF⊥EH于F,设DF=a米,根据直角三角形的性质用a表示出CF、CD,根据正切的定义求出BE,根据题意列方程,解方程得到答案.
解:作DG⊥AE于G,DF⊥EH于F,
则四边形GEFD为矩形,
∴GE=DF,GD=EF,
设DF=a米,则GE=a,
在Rt△DCF中,∠DCF=30°,
∴CD=2DF=2a,CF=![]() a,
a,
∴EF=EC+CF=120![]() +
+![]() a,
a,
∵AM∥GD,
∴∠ADG=∠MAD=45°,
∴AG=DE=EF=120![]() +
+![]() a,
a,
∵BN∥EF,
∴∠BCE=∠NBC=60°,
在Rt△BEC中,tan∠BCE=![]() ,
,
BE=ECtan60°=120![]() ×
×![]() =360,
=360,
AG=AB+BE﹣GE=450﹣a,
∴450﹣a=120![]() +
+![]() a,
a,
解得,a=285![]() ﹣405,
﹣405,
∴CD=2a=570![]() ﹣810,
﹣810,
答:山体滑坡的坡面长度CD的长为(570![]() ﹣810)米.
﹣810)米.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
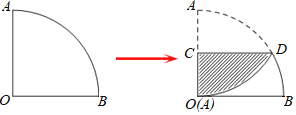
【题目】如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为( )
A. 6π﹣![]() B. 6π﹣9
B. 6π﹣9![]() C. 12π﹣
C. 12π﹣![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“学习朱子文化,弘扬理学思想”为主题的读书月活动,并向学生征集读后感,学校将收到的读后感篇数按年级进行统计,绘制了以下两幅统计图(不完整).
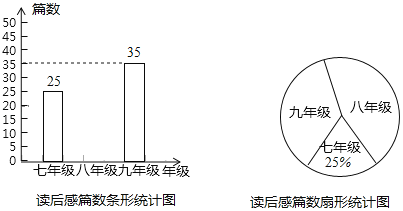
据图中提供的信息完成以下问题
(1)扇形统计图中“八年级”对应的圆心角是 °,并补全条形统计图;
(2)经过评审,全校有4篇读后感荣获特等奖,其中有一篇来自七年级,学校准备从特等奖读后感中任选两篇在校广播电台上播出,请利用画树状图或列表的方法求出七年级特等奖读后感被校广播电台播出的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
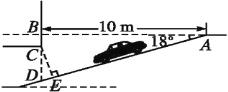
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC与△DEF均为等边三角形,且AB=2,DB=1,现△ABC静止不动,△DEF沿着直线EC以每秒1个单位的速度向右移动设△DEF移动的时间为x,△DEF与△ABC重合的面积为y,则能大致反映y与x函数关系的图象是( )
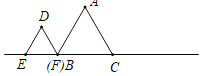
A.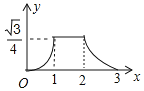 B.
B.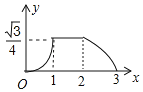
C.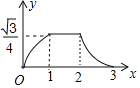 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有_____.(填序号)
①![]() 的平方根是±3
的平方根是±3
②绝对值等于它本身的数一定是正数
③关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是m≤3
④如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是8
⑤观察下列单项式2x,﹣4x2,8x3,﹣16x4,…,则第7个单项式是128x7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义.
(2)求线段AB所表示的y1与x之间的函数表达式.
(3)当0≤x≤90时,销售该产品获得的利润与产量的关系式是 ;当90≤x≤130时,销售该产品获得的利润与产量的关系式是 ;总之,当产量为 kg时,获得的利润最大,最大利润是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com