
【题目】如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为( )
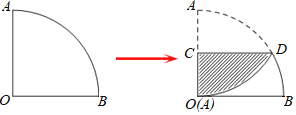
A. 6π﹣![]() B. 6π﹣9
B. 6π﹣9![]() C. 12π﹣
C. 12π﹣![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF,
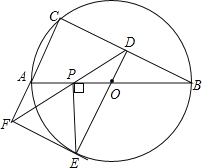
(1)求证:OD=OP;(2)求证:FE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
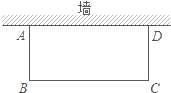
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
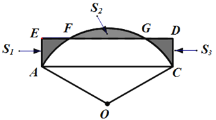
【题目】如图,半径为3的扇形AOB,∠AOB=120°,以AB为边作矩形ABCD交弧AB于点E,F,且点E,F为弧AB的四等分点,矩形ABCD与弧AB形成如图所示的三个阴影区域,其面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() 为( )(
为( )(![]() 取
取![]() )
)
A. ![]()
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
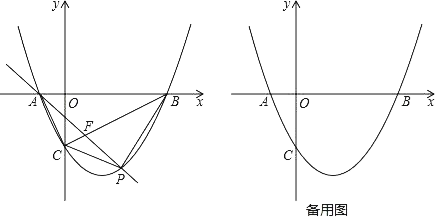
(1)求A,B两点的坐标.
(2)点P是线段BC下方的抛物线上的动点,连结PC,PB.
①是否存在一点P,使△PBC的面积最大,若存在,请求出△PBC的最大面积;若不存在,试说明理由.
②连结AC,AP,AP交BC于点F,当∠CAP=∠ABC时,求直线AP的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前中学生带手机进校园现象越来越受到社会关注,针对这种现象,某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
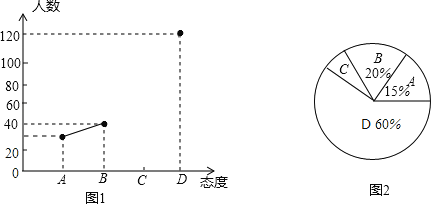
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计1万名中学生家长中有多少名家长持反对态度;
(4)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 与一次函数y=kx+b(k≠0)交于点A(﹣1,6)、B(n,2).
与一次函数y=kx+b(k≠0)交于点A(﹣1,6)、B(n,2).
(1)求反比例函数与一次函数的表达式;
(2)若点A关于y轴的对称点为A′,连接AA′,BA′,求△AA′B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
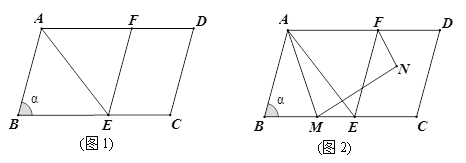
【题目】如图1,在□ABCD中,AB=6,∠B= ![]() (60°<
(60°<![]() ≤90°). 点E在BC上,连接AE,把△ABE沿AE折叠,使点B与AD上的点F重合,连接EF.
≤90°). 点E在BC上,连接AE,把△ABE沿AE折叠,使点B与AD上的点F重合,连接EF.
(1)求证:四边形ABEF是菱形;
(2)如图2,点M是BC上的动点,连接AM,把线段AM绕点M顺时针旋转![]() 得到线段MN,连接FN,求FN的最小值(用含
得到线段MN,连接FN,求FN的最小值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
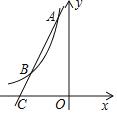
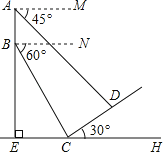
【题目】夏季多雨,在山坡CD处出现了滑坡,为了测量山体滑坡的坡面长度CD,探测队在距离坡底C点![]() 米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com